概述
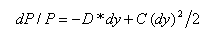 凸性
凸性久期描述了價格-收益率曲線的斜率,凸性描述了價格/收益率曲線的彎曲程度。凸性是債券價格對收益率的二階導數。
凸性的計算
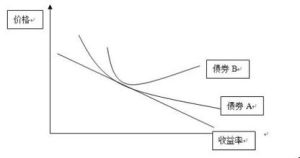
由債券定價定理1與4可知,債券價格-收益率曲線是一條從左上向右下傾斜,並且下凸的曲線。下圖中b>a。
債券定價定理1:
債券價格與到期收益率成反向關係。
若到期收益率大於息票率,則債券價格低於面值,稱為折價債券(discount bonds);
若到期收益率小於息票率,則債券價格高於面值,稱為溢價債券(premium bonds);
若息票率等於到期收益率,則債券價格等於面值,稱為平價債券(par bonds)。
對於可贖回債券,這一關係不成立。
債券定價定理4:
若債券期限一定,同等收益率變化下,債券收益率上升導致價格下跌的量,要小於收益率下降導致價格上升的量。
例:三債券的面值都為1000元,到期期限5年,息票率7%,當到期收益率變化時。
到期收益率(%) 6 7 8
價格 1042.12 1000 960.07
債券價格變化率(%) 4.21 0 -4.00
凸性的性質
1、凸性隨久期的增加而增加。若收益率、久期不變,票面利率越大,凸性越大。利率下降時,凸性增加。
2、對於沒有隱含期權的債券來說,凸性總大於0,即利率下降,債券價格將以加速度上升;當利率上升時,債券價格以減速度下降。
3、含有隱含期權的債券的凸性一般為負,即價格隨著利率的下降以減速度上升,或債券的有效持續期隨利率的下降而縮短,隨利率的上升而延長。因為利率下降時買入期權的可能性增加了。
凸性是對債券價格利率敏感性的二階估計,是對債券久期利率敏感性的測量。在價格-收益率出現大幅度變動時,它們的波動幅度呈非線性關係。由持久期作出的預測將有所偏離。凸性就是對這個偏離的修正。它由以下公式定義:
無論收益率是上升還是下降,凸性所引起的修正都是正的。因此如果修正持久期相同,凸性越大越好。凸性的計算公式為:
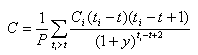 凸性
凸性