不變測度亦稱平穩分布，是 E 上的一種機率分布，它使馬爾可夫過程成為平穩隨機過程。
不變測度亦稱平穩分布(stationary distribution)。
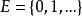不變測度
不變測度
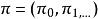不變測度不變測度是E 上的一種機率分布，它使馬爾可夫過程成為平穩隨機過程。給定以 為狀態空間的時齊馬爾可夫鏈 ，其一步轉移陣為 P。如果存在 E 上的機率分布 ，滿足矩陣方程
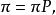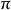不變測度
不變測度則稱 為鏈的平穩分布，或稱為轉移陣 P 的不變測度。
不變測度具有性質：
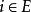不變測度
不變測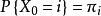度
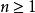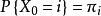不變測度 不變測度若鏈以它為初始分布，即每個 有 ，那么此過程的有窮維分布是推移不變的（即強平穩的）。特別地，對一切 永有 。馬爾可夫鏈有平穩分布的充分必要條件是它有常返狀態。
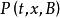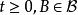不變測度
不變測度一般地，以 為轉移機率分布的時齊馬爾可夫過程的不變測度定義為相空間（E，ℬ）上滿足如下條件的測度μ：任意的 有
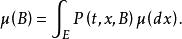不變測度零測度就是某個集合的測度為0。數學上，測度（Measure）是一個函式，它對一個給定集合的某些子集指定一個數，這個數可以比作大小、體積、機率等等。
測度 測度的定義 性質 σ-有限測度 完備性數學上，測度（Measure）是一個函式，它對一個給定集合的某些子集指定一個數，這個數可以比作大小、體積、機率等等。傳統的積分是在區間上進行的，後來人們...
定義 性質 完備性 例子哈爾測度，局部緊群 G上的在左(右)平移作用下不變的非負(不恆為0)正規波萊爾測度稱為G的左(右)哈爾測度。所謂“平移作用下的不變測度”的含意可以有兩種等價理解。
哈爾測度 正文 配圖 相關連線哈爾測度是不恆等於零的不變測度，Rn上的勒貝格測度在拓撲群上的推廣。設G是局部緊豪斯多夫拓撲群，Ω=G，sx(或xs)是群G內的乘法。此時把G上的非零左...
人物簡介 概念介紹 預備知識 哈爾定理 數理統計中的套用哈爾測度，局部緊群 G上的在左(右)平移作用下不變的非負(不恆為0)正規波萊爾測度稱為G的左(右)哈爾測度。所謂“平移作用下的不變測度”的含意可以有兩種等價理解。
哈爾測度 正文 配圖 相關連線《系統重要性測度原理與套用》是2014年11月出版的圖書，作者是苗強、王冬。
內容簡介 圖書目錄擬不變測度 ...
1.2 2.1 2.3
基本信息 內容簡介 編輯推薦 目錄 序言西奈-呂埃爾-鮑恩測度 (Sinai-Ruelle-Bowenmeasure)簡稱SRB測度，是公理A微分同胚在其吸引子上的一個具有物理意義的不變測度。
