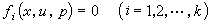一階偏微分方程
正文
最簡單的一類偏微分方程。一個未知函式u(x)=u(x1,x2,…, xn)所適合的一組一階偏微分方程即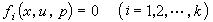 , (1)
, (1)
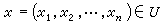 (Rn之開集),u是實值函式,
(Rn之開集),u是實值函式,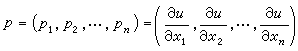 。適合(1)的函式u稱為其解。單個擬線性方程
。適合(1)的函式u稱為其解。單個擬線性方程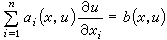 (2)
(2)
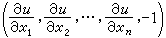 是其上一點(x,u)處的法線方向數,(α1,α2,…,αn,b))則定義一個方向場,稱為特徵方向場。式(2)表明積分曲面在其各點上均與該方向場相切。特徵方向場的積分曲線,稱為(2)的特徵曲線。它們是常微分方程組(特徵方程)
是其上一點(x,u)處的法線方向數,(α1,α2,…,αn,b))則定義一個方向場,稱為特徵方向場。式(2)表明積分曲面在其各點上均與該方向場相切。特徵方向場的積分曲線,稱為(2)的特徵曲線。它們是常微分方程組(特徵方程) 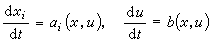 (3)
(3)
式(2)的定解問題中,最重要的是柯西問題,即在U中給定一個n-1維子流形 у及其上的函式φ(x),要求式(2)的解u=u(x)滿足以下的附加條件(初始條件):
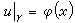 。 (4)
。 (4)
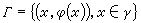 是U×R中一個給定的n-1維子流形,而條件(4)即要求積分曲線(它是U×R中的一個n維子流形)通過Γ。
是U×R中一個給定的n-1維子流形,而條件(4)即要求積分曲線(它是U×R中的一個n維子流形)通過Γ。 柯西問題的解的局部存在的條件從幾何上看是很清楚的:若在(x0, u0)∈Γ附近
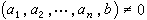 ,則在該點附近特徵向量場微分同胚於平行向量場,特徵曲線族則微分同胚於平行直線族。如果Γ在(x0,u0)附近橫截(即不平行)於該平行直線族,就可以以Γ為底,以該平行直線為“母線”作一“柱面”。它就是所求的積分曲面,亦即柯西問題的解。
,則在該點附近特徵向量場微分同胚於平行向量場,特徵曲線族則微分同胚於平行直線族。如果Γ在(x0,u0)附近橫截(即不平行)於該平行直線族,就可以以Γ為底,以該平行直線為“母線”作一“柱面”。它就是所求的積分曲面,亦即柯西問題的解。 對一般的單個一階非線性偏微分方程
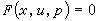 , (5)
, (5)
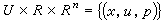 代替上述的U×R。對於積分曲面u=u(x),它在(x,u(x))處的法線方向由
代替上述的U×R。對於積分曲面u=u(x),它在(x,u(x))處的法線方向由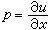 所確定,因此(x,u,p)決定了一個過(x,u)的以
所確定,因此(x,u,p)決定了一個過(x,u)的以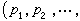
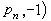 為法線的超平面,即過該點的積分曲面的切超平面。於是,在U×R中來看,{(x, u,p)}給出一個超平面場,每一個這樣的超平面稱為過(x, u)的接觸元素。對於給定的(x, u),適合方程(5)的p不是惟一的,從而有一個接觸元素族。它們的包絡是一個以(x, u)為頂點的錐,稱為蒙日錐。方程(5)的積分曲面在各點均切於過該點的蒙日錐。
為法線的超平面,即過該點的積分曲面的切超平面。於是,在U×R中來看,{(x, u,p)}給出一個超平面場,每一個這樣的超平面稱為過(x, u)的接觸元素。對於給定的(x, u),適合方程(5)的p不是惟一的,從而有一個接觸元素族。它們的包絡是一個以(x, u)為頂點的錐,稱為蒙日錐。方程(5)的積分曲面在各點均切於過該點的蒙日錐。 對於擬線性方程(2),蒙日錐蛻化為過(x,u)的以
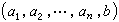 為方向的軸。
為方向的軸。 積分曲面既切於蒙日錐,則必沿某一母線切於它。這條母線的方向給出了積分曲面上的一個方向場。對於方程(2)來看,它就是特徵方向場。所以在一般的非線性方程(5),也稱它為特徵方向場,其積分曲線也稱為方程(5)的特徵曲線。積分曲面仍由特徵曲線織成。
但是,與方程(2)也有所不同,即現在必須在U×R×Rn中來考慮特徵方向場,從而可以得到如下的常微分方程組
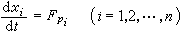 , (6)
, (6)
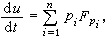 (7)
(7)
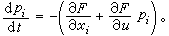 (8)
(8)
解柯西問題的特徵線法 在解柯西問題(4)時,將у寫成參數形式
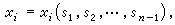 (9)
(9)
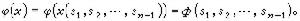 (10)
(10)
對於擬線性方程(2),以(9)、(10)為初始條件解特徵方程組(3),可得
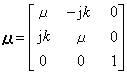 (11)
(11)
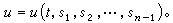 (12)
(12)
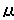
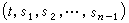 為 (x1,x2,…, xn)的函式,代入(12)即得柯西問題的解。在以上討論中,條件
為 (x1,x2,…, xn)的函式,代入(12)即得柯西問題的解。在以上討論中,條件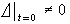 (13)
(13)
對於非線性偏微分方程(5),需要解出特徵帶的方程組(6)、(7)、(8)。這時需要 pj所適合的初始條件。很容易看到,在t=0時,pj應適合以下條件
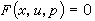 , (14)
, (14)
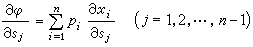 。 (15)
。 (15)
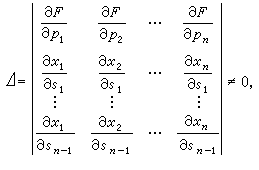 (16)
(16)
若帶條件和特徵條件得以滿足,就將得出在 t=0時xj、u和pj所適合的初始條件。於是可以得到
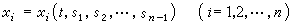 , (17)
, (17)
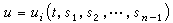 , (18)
, (18)
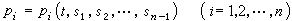 , (19)
, (19)
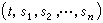 為(x1,x2,…,xn)的函式,代入式(18)即得u=u(x)為柯西問題的解。代入式(19)得pj=pj(x),可以證明恰好有
為(x1,x2,…,xn)的函式,代入式(18)即得u=u(x)為柯西問題的解。代入式(19)得pj=pj(x),可以證明恰好有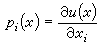 。
。 拉格朗日-查皮特方法 求解柯西問題(5)、(4)的另一方法,是求(5)的含有n個參數α=( α1, α2,…, αn)的解u=u(x,α)。它稱為(5)的完全積分。
將(4)所定義的子流形Γ局部地表為
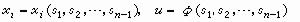 。
。
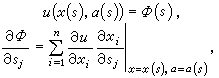
若將完全積分對n個α求包絡,即由
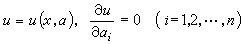
於是問題歸結為如何求完全積分。為此考慮一個與之相關的問題:求函式u=u(x)使之滿足一組偏微分方程
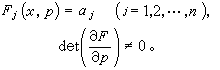 (20)
(20)
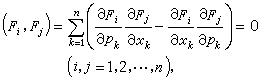 (21)
(21)
方程(5)可以化為不顯含u的情形。因為若將u=u(x)寫為隱函式v(x,u)=с,而以v為新的未知函式,則(5)成為
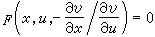 。若視u為自變數則未知函式v不顯現。因此可以限於求解以下形式的方程
。若視u為自變數則未知函式v不顯現。因此可以限於求解以下形式的方程 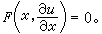 (22)
(22)
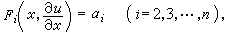 (23)
(23)
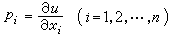 (其中含常數α2,α3,…,αn),即可得(5)的含有n個常數的解(即完全積分)
(其中含常數α2,α3,…,αn),即可得(5)的含有n個常數的解(即完全積分) 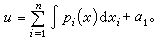
普法夫方程組、費羅貝尼烏斯條件 在 U嶅Rn中若給定了一個充分光滑的向量場,則過U之每一點必有其惟一的積分曲線。若給定r(1<r<n)個光滑向量場,則不一定經過每一點都有 r維子流形使得在其各點上均與這些向量場相切(也不一定能找到 n-1維子流形使得在其各點上均與這些向量場相切)。若有這樣的 r維子流形存在,就說這些向量場可積,該流形稱為其積分流形。
求積分流形發生障礙的幾何原因,可由下例看出。設在R3中給出一個平面場(相當於兩個向量場),作柱面如圖
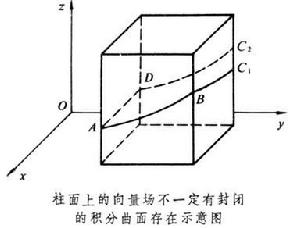 ,則該平面場在柱面上決定一個向量場。若原平面場可積而有積分曲面存在,則積分曲面與柱面相截將給出柱面上的向量場的封閉積分曲線。但是柱面上的向量場不一定有封閉的積分曲面存在。
,則該平面場在柱面上決定一個向量場。若原平面場可積而有積分曲面存在,則積分曲面與柱面相截將給出柱面上的向量場的封閉積分曲線。但是柱面上的向量場不一定有封閉的積分曲面存在。 上述問題稍加改述:求一個超曲面u=u(x)(而不只是r維子流形)與r個向量場相切,即
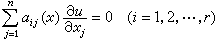 , (24)
, (24)
式(24)規定出 r個一階偏微分運算元(亦即向量場)
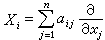 。它們的交換子仍是一階偏微分運算元:
。它們的交換子仍是一階偏微分運算元: 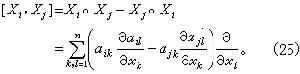
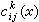 使得
使得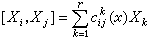 滿足式(25)的向量場x1,x2,…,xr稱為對合的。
滿足式(25)的向量場x1,x2,…,xr稱為對合的。 一階偏微分方程的幾何理論有悠久的歷史淵源,以後經過É.(-J.)嘉當等人的發展,在幾何學、力學和物理學中都有重大的意義。