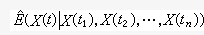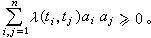正態過程

有窮維分布都是常態分配的隨機過程,又稱高斯過程。就象一維常態分配被它的均值（見數學期望）和方差所確定一樣,正態過程{x(t),t∈T}被它的均值函式m(t)=Ex(t)和協方差函式　λ(s,t)=Ex(s)x(t)-m(s)m(t)
所確定，其中λ(s，t)是對稱非負定函式，即λ(s，t)=λ(t,s)，而且對任意的 tj∈T及實數αj，1≤i≤n，有

隨機過程

反之,對任給的有限實值函式m(t)和對稱非負定函式λ(s,t),由柯爾莫哥洛夫定理可證,存在一個正態過程，以m(t)為其均值函式，以λ(s,t)為其協方差函式。
根據中心極限定理，許多實際問題中出現的隨機過程可近似地視為正態過程。此外，正態過程有一系列的好性質,如它的最佳線性估計重合於條件期望,這一點在套用上是很方便的，既準確又便於計算。因此正態過程在實際中有廣泛的套用，在無線電通訊及自動控制中尤為重要。為方便計,設m(t)呏0。任取tj,t∈T,用L(x(t1),x(t2), …,x(tn))表示由x(t1),x(t2),…,x(tn)的線性組合所構成的希爾伯特空間，x(t)在此空間上的投影記作

稱為x(t)關於x(t1)，x(t2),…，x(tn)的最佳線性估計,即線性最小均方誤差估計;條件期望E(x(t)|x(t1),x(t2),…，x(tn))則是非線性的最小均方誤差估計。對正態過程來講，這兩種估計以機率1相等。