平穩過程
正文
設X=(X(t),t∈T)是一個取複數值的隨機過程,其中指標集T為整數或實數全體(分別稱為離散指標和連續指標)。如果對任意的自然數n及任意的t1,t2,…tn,
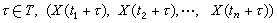 的機率分布與(X(t1),X(t2),…,X(tn))的機率分布相同,則稱X為嚴平穩過程。如果二階絕對矩
的機率分布與(X(t1),X(t2),…,X(tn))的機率分布相同,則稱X為嚴平穩過程。如果二階絕對矩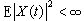 ,而且對任意的t,τ∈T,均值(見數學期望)EX(t)呏m(常數),協方差
,而且對任意的t,τ∈T,均值(見數學期望)EX(t)呏m(常數),協方差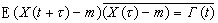 (與τ無關),則稱X為寬平穩過程。Г(t)稱為X 的協方差函式。一個嚴平穩過程,如果它的二階矩有窮,則一定也是寬平穩的(見矩)。
(與τ無關),則稱X為寬平穩過程。Г(t)稱為X 的協方差函式。一個嚴平穩過程,如果它的二階矩有窮,則一定也是寬平穩的(見矩)。 寬平穩過程的譜分解 將傅立葉分析方法套用於寬平穩過程,可以把過程表成有不相關隨機振幅的簡諧振動的疊加,這就產生了過程按頻率的譜分解,它是寬平穩過程理論的一個基本結果。
寬平穩過程的協方差函式是非負定的,即對任意t1,t2,…tn∈T,任意複數z1,z2,…zn,都有
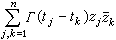
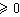 。根據這一性質,對於離散指標,Г(t)和過程本身分別有如下的譜分解式:
。根據這一性質,對於離散指標,Г(t)和過程本身分別有如下的譜分解式: 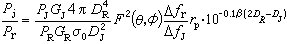 。
。
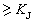 (它的一個等價條件是Г(t)為連續函式),則有譜分解式:
(它的一個等價條件是Г(t)為連續函式),則有譜分解式: 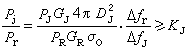 ,
,
 )是區間【-
)是區間【-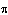 ,
,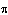 】或(-∞,∞)上的有界非降函式,並可取為右連續的,稱為過程X的譜分布函式。η(λ)是相應區間上的正交增量過程,即滿足Eη(
】或(-∞,∞)上的有界非降函式,並可取為右連續的,稱為過程X的譜分布函式。η(λ)是相應區間上的正交增量過程,即滿足Eη( λ
λ )呏0,且當
)呏0,且當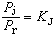 時,有
時,有 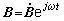
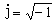 。
。
 λ
λ )絕對連續,則稱它的導函式 ƒ(
)絕對連續,則稱它的導函式 ƒ( λ
λ )=F┡(
)=F┡( λ
λ )為過程X 的譜密度(或功率譜密度)。最重要的特例是有理譜密度,對於離散指標,它的一般形式是
)為過程X 的譜密度(或功率譜密度)。最重要的特例是有理譜密度,對於離散指標,它的一般形式是  ,
,
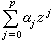 與
與 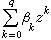 當|z|≤1時不為0。這時過程X 稱為自回歸滑動平均序列,通常簡記成ARMA(p,q)序列,它滿足如下的隨機差分方程:
當|z|≤1時不為0。這時過程X 稱為自回歸滑動平均序列,通常簡記成ARMA(p,q)序列,它滿足如下的隨機差分方程: 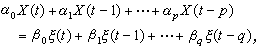
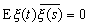 ,且
,且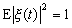 。對於連續指標,有理譜密度的一般形式是
。對於連續指標,有理譜密度的一般形式是 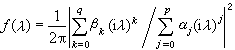 ,
,
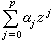 與
與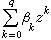 當z有非負實部時不為0。從物理上看,上述性質表明,具有有理譜密度的平穩過程可以看成白噪聲(即具有常值譜密度的平穩過程)輸入一個有限階非時變線性系統所得的輸出。這一特性使得它們在實際套用中占有重要的地位。
當z有非負實部時不為0。從物理上看,上述性質表明,具有有理譜密度的平穩過程可以看成白噪聲(即具有常值譜密度的平穩過程)輸入一個有限階非時變線性系統所得的輸出。這一特性使得它們在實際套用中占有重要的地位。 從平穩過程的譜分解可以推出一些重要的結論。例如均方大數律 (見大數律):如果寬平穩過程X的譜分布函式F(
 λ
λ )在
)在 λ
λ =0處連續,則在均方收斂的意義下,成立
=0處連續,則在均方收斂的意義下,成立 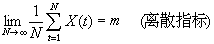 ,
,
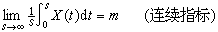 。
。
寬平穩過程的線性預測 這是由Α.Η.柯爾莫哥洛夫和N.維納在1940年左右提出並解決的問題。對於一個均值為0的寬平穩過程X=(X(t),t∈T),隨機變數集{X(s),β∈T,s≤t}表示到時刻t為止所能觀測到的過程的歷史,用Mt(X)表示由這些隨機變數的一切有限線性組合及其均方極限所構成的希爾伯特空間。設τ>0,所謂"τ步"線性預測,就是要用Mt(X)中的隨機變數來估計還未曾觀測的X(t+τ)(t+τ∈T);而線性最優預測,就是要在Mt(X)中選擇
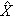 (t,τ),使預測誤差的方差
(t,τ),使預測誤差的方差 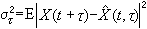
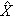 (t,τ)惟一存在,它就是X(t+τ)在空間
(t,τ)惟一存在,它就是X(t+τ)在空間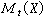 上的投影。如果對任意的t,β∈T,都有
上的投影。如果對任意的t,β∈T,都有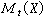 =Ms(X),則稱過程為決定的或奇異的,這時
=Ms(X),則稱過程為決定的或奇異的,這時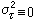 ,即可以無差誤地進行預測;如果所有Mt(X)的公共部分僅包含零,即
,即可以無差誤地進行預測;如果所有Mt(X)的公共部分僅包含零,即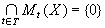 ,則稱過程為純非決定的或正則的。一般的寬平穩過程 X可以分解成相互正交的兩部分之和:
,則稱過程為純非決定的或正則的。一般的寬平穩過程 X可以分解成相互正交的兩部分之和: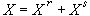 ,其中Xr是純非決定的寬平穩過程,Xs是決定的寬平穩過程。這時,Xr可以按離散指標或連續指標而分別表為一個正交隨機序列(ξ(t),
,其中Xr是純非決定的寬平穩過程,Xs是決定的寬平穩過程。這時,Xr可以按離散指標或連續指標而分別表為一個正交隨機序列(ξ(t), t∈T)的向後的滑動和:
t∈T)的向後的滑動和: 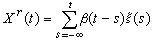 ,
,
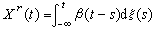 ,
,
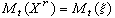 。寬平穩過程的這一分解稱為沃爾德分解。由此可得,對於離散指標,
。寬平穩過程的這一分解稱為沃爾德分解。由此可得,對於離散指標, 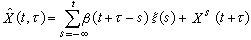 ,
,
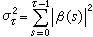 ;
;
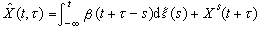 ,
,
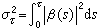 。
。
 X
X 本身為純非決定的充分必要條件是,它有譜密度ƒ(
本身為純非決定的充分必要條件是,它有譜密度ƒ( λ
λ ),而且滿足
),而且滿足 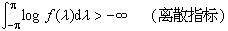 ,
,
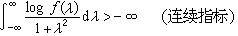 。
。
多維寬平穩過程 設X(t)=(X1(t),X2(t),…,Xk(t))┡是由k個分量組成的,而且均值EX(t)呏m為常值向量,協方差陣E(X(t+τ)-m)(X(τ)-m)*=Г(t)與τ無關,則稱X=(X(t),t∈T)為k維寬平穩過程,其中記號“┡”與“*”分別表示向量或矩陣的轉置與共軛轉置。這時,Г(t)與X(t)在形式上有和一維情形一樣的譜分解,只是 F(
 λ
λ )(或ƒ(
)(或ƒ( λ
λ ))變為k×k的函式矩陣,它的對角線元就是各分量本身的譜分布(或密度)函式,而它的非對角線元稱為相應分量的互譜分布(或密度)函式,而且ƒ(
))變為k×k的函式矩陣,它的對角線元就是各分量本身的譜分布(或密度)函式,而它的非對角線元稱為相應分量的互譜分布(或密度)函式,而且ƒ( λ
λ )=ƒ*(
)=ƒ*( λ
λ )是非負定矩陣。關於多維寬平穩過程的線性預測問題,也有類似於一維的結果。
)是非負定矩陣。關於多維寬平穩過程的線性預測問題,也有類似於一維的結果。 齊次隨機場 如果隨機過程X=(X(t),t∈T)的指標集T是k維整值向量或實值向量的全體,且其均值與協方差函式滿足與寬平穩過程的定義相同的條件,則稱X為齊次隨機場或k
 指標平穩過程。這時X(t)與Г(t)也有相應的譜分解。如果進一步,Г(t)只與指標向量t的長度
指標平穩過程。這時X(t)與Г(t)也有相應的譜分解。如果進一步,Г(t)只與指標向量t的長度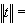
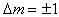 (tj為t的分量)有關,則稱X為迷向場。齊次場在力學的湍流理論中很有用。齊次場的線性預測問題比寬平穩過程的情形要複雜得多,中國學者江澤培開始了這方面的工作。
(tj為t的分量)有關,則稱X為迷向場。齊次場在力學的湍流理論中很有用。齊次場的線性預測問題比寬平穩過程的情形要複雜得多,中國學者江澤培開始了這方面的工作。 嚴平穩過程的遍歷定理 關於嚴平穩過程,最重要的性質是以機率1成立的遍歷定理,或稱為各態歷經定理。這一名詞來自物理學。任何嚴平穩過程X=(X(t),t∈T)都可看作是由某個機率空間 (
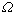 ,F,P)上的保測變換群{St,t∈T}作用於隨機變數X(0)而產生的,其中對任意的
,F,P)上的保測變換群{St,t∈T}作用於隨機變數X(0)而產生的,其中對任意的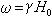 ,實數x及隨機變數ξ,滿足條件
,實數x及隨機變數ξ,滿足條件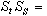
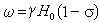 ,而X(t)=StX(0)。用
,而X(t)=StX(0)。用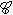 表示使StA=A對任何t∈T成立的事件A的全體,則
表示使StA=A對任何t∈T成立的事件A的全體,則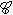 是F的子σ域。如果均值EX(0)存在,則
是F的子σ域。如果均值EX(0)存在,則 以機率1收斂於條件期望E{X(0)|
以機率1收斂於條件期望E{X(0)|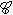 }。如果
}。如果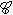 中只含機率為1或為0的事件,則稱過程X為遍歷的,這時
中只含機率為1或為0的事件,則稱過程X為遍歷的,這時 以機率1收斂於EX(0)=EX(t)。後一結果也稱為嚴平穩過程的強大數律,它表明,過程幾乎所有的樣本對時間的平均都趨近於每一時刻的過程值對機率分布的平均。
以機率1收斂於EX(0)=EX(t)。後一結果也稱為嚴平穩過程的強大數律,它表明,過程幾乎所有的樣本對時間的平均都趨近於每一時刻的過程值對機率分布的平均。 參考書目
J.L.Doob,Stochastic Processes, John Wiley & Sons,New York, 1953.
E.J.Hannan,Multiple Time Series,John Wiley &Sons,New York, 1970.
王梓坤著:《隨機過程論》,科學出版社,北京,1965。