數學術語
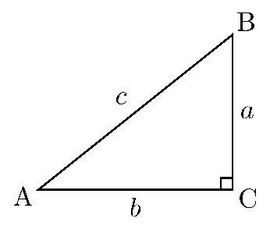
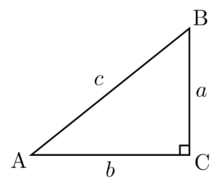
某直角三角形中，一個銳角的斜邊與其鄰邊的比（即角A斜邊比鄰邊）,叫做該銳角的正割，用 sec（角）表示 。如設該直角三角形各邊為a，b，c，則secA=c/b.
正割（sec的完整形式為secant）
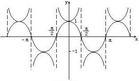
在y=secx中，以x的任一使secx有意義的值與它對應的y值作為(x，y)．在直角坐標系中作出的圖形叫正割函式的圖像，也叫正割曲線．
正割性質
y=secx的性質
(1)定義域,{x|x≠kπ+π/2，k∈Z}
(2)值域,|secx|≥1．即secx≥1或secx≤－1；
(3)y=secx是偶函式，即sec(－x)=secx．圖像對稱於y軸；
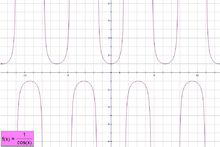正割繪圖(4)y=secx是周期函式．周期為2kπ(k∈Z，且k≠0)，最小正周期T=2π．
正割與餘弦互為倒數，餘割與正弦互為倒數。
（5）secθ=1/cosθ
| 正割 | |
 | |
| 性質 | |
| 奇偶性 | 偶 |
| 定義域 | {x|x≠kπ+π/2，k∈Z} |
| 到達域 | |secx|≥1 |
| 周期 | 2π |
| 特定值 | |
| 當x=0 | 1 |
| 當x=+∞ | N/A |
| 當x=-∞ | N/A |
| 最大值 | ∞ |
| 最小值 | -∞ |
| 其他性質 | |
| 漸近線 | N/A |
| 根 | 無實根 |
| 臨界點 | kπ |
| 拐點 | (kπ,0) |
| 不動點 | 0 |
| k是一個 整數 . | |
單位圓定義
正割圖像中給出了用弧度度量的某個公共角。逆時針方向的度量是正角而順時針的度量是負角。設一個過原點的線，同 x 軸正半部分得到一個角 θ，並與單位圓相交。這個交點的 y 坐標等於 sin θ。在這個圖形中的三角形確保了這個公式；半徑等於斜邊並有長度 1，所以有了 sec θ = 1/x 。單位圓可以被認為是通過改變鄰邊和對邊的長度並保持斜邊等於 1 查看無限數目的三角形的一種方式。
級數定義
正割也能使用泰勒級數來定義:
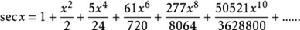正割