簡介
帕德是法國數學家亨利·帕德發明的有理多項式近似法。帕德近似往往比截斷的泰勒級數準確，而且當泰勒級數不收斂時，帕德近似往往仍可行，所以多用於在計算機數學中。
例如， 1/（1-x) 的泰勒級數
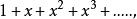帕德逼近只當 -1<x<1 時收斂，不如原函式廣泛。
定義
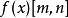帕德逼近給定兩個正整數m、n, 函式 階帕德近似為
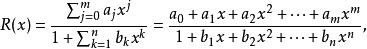帕德逼近並且
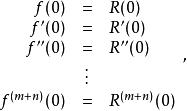帕德逼近
帕德逼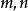近
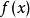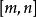帕德逼近
帕德逼近對於給定的 函式 的 階帕德近似是唯一的 。
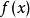帕德逼近函式 的帕德近似記為
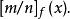帕德逼近它不僅與逼近論中其他許多方法有著密切的關係，而且在實際問題特別是許多物理問題中有著廣泛的套用。設是在原點某鄰域內收斂的、具有復係數的馬克勞林級數。欲確定一個有理函式，式中,使得前次方的係數為0，即使得此處約定qk=0（k>n）。雖然所求得的Pm(z)和Qn(z)不惟一，但是比式卻總是惟一的。有理函式稱為F(z)的(m,n)級帕德逼近，記為[m/n]。由[m/n]所形成的陣列稱為帕德表。
例子
正弦函式
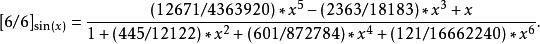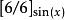帕德逼近
帕德逼近的6+6=12階泰勒級數展開為
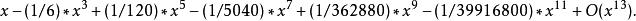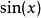帕德逼近
帕德逼近和 的12階泰勒級數全同：
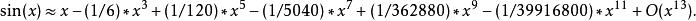帕德逼近指數函式
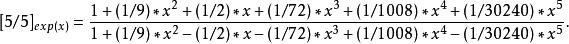帕德逼近其泰勒級數為
帕德逼近與exp(x)本身的泰勒級數展開的前10階完全等同：
帕德逼近•又如
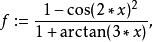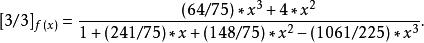帕德逼近
帕德逼近雅可比橢圓函式
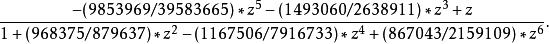帕德逼近第一類 5 階貝塞爾函式
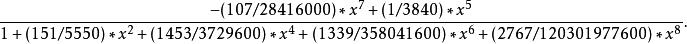帕德逼近誤差函式
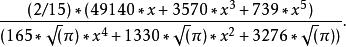帕德逼近菲涅耳積分
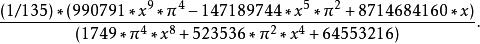帕德逼近