概念
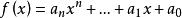 同餘方程
同餘方程定義1:設是整係數多項式,稱
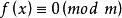 同餘方程
同餘方程 同餘方程
同餘方程 同餘方程
同餘方程 同餘方程
同餘方程是關於未知數的模的同餘方程,簡稱為模的同餘方程。
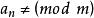 同餘方程
同餘方程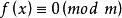 同餘方程
同餘方程 同餘方程
同餘方程若,則稱為次同餘方程。
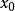 同餘方程
同餘方程 同餘方程
同餘方程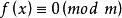 同餘方程
同餘方程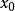 同餘方程
同餘方程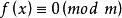 同餘方程
同餘方程 同餘方程
同餘方程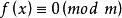 同餘方程
同餘方程 同餘方程
同餘方程 同餘方程
同餘方程定義2:設是整數,當時,成立,則稱是同餘方程的解。凡對於模同餘的解,被視為同一個解。同餘方程的解數是指它的關於模互不相余的所有解的個數,也即在模的一個完全剩餘系中的解的個數。
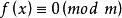 同餘方程
同餘方程 同餘方程
同餘方程由定義2,同餘方程的解數不超過。
基本原理
定理:下面的結論成立:
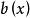 同餘方程
同餘方程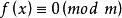 同餘方程
同餘方程(1)設是整係數多項式,則同餘方程與
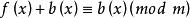 同餘方程
同餘方程等價;
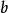 同餘方程
同餘方程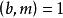 同餘方程
同餘方程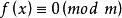 同餘方程
同餘方程(2)設是整數,,則同餘方程與
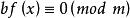 同餘方程
同餘方程等價;
 同餘方程
同餘方程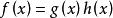 同餘方程
同餘方程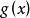 同餘方程
同餘方程 同餘方程
同餘方程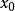 同餘方程
同餘方程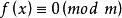 同餘方程
同餘方程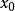 同餘方程
同餘方程(3)設是素數,,與都是整係數多項式,又設是同餘方程的解,則必是同餘方程
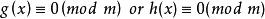 同餘方程
同餘方程的解。
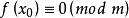 同餘方程
同餘方程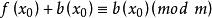 同餘方程
同餘方程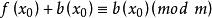 同餘方程
同餘方程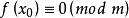 同餘方程
同餘方程證明:(1)若,則成立,反之,若,則成立;
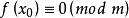 同餘方程
同餘方程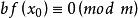 同餘方程
同餘方程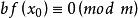 同餘方程
同餘方程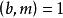 同餘方程
同餘方程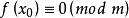 同餘方程
同餘方程(2)若,則成立,反之,若,則由得成立;
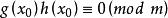 同餘方程
同餘方程 同餘方程
同餘方程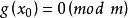 同餘方程
同餘方程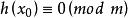 同餘方程
同餘方程(3)若,則由是素數得或。證畢。

