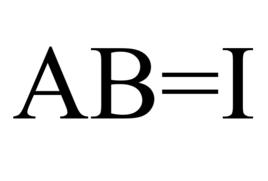定義
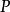 可逆矩陣
可逆矩陣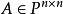 可逆矩陣
可逆矩陣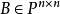 可逆矩陣
可逆矩陣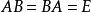 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣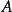 可逆矩陣
可逆矩陣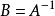 可逆矩陣
可逆矩陣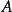 可逆矩陣
可逆矩陣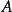 可逆矩陣
可逆矩陣設是數域,,若存在,使得,為單位陣,則稱為可逆陣,為的逆矩陣,記為。若方陣的逆陣存在,則稱為可逆矩陣或非奇異矩陣。
性質
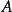 可逆矩陣
可逆矩陣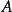 可逆矩陣
可逆矩陣(1)若為可逆矩陣,則的逆矩陣是唯一的。
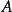 可逆矩陣
可逆矩陣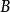 可逆矩陣
可逆矩陣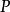 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣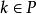 可逆矩陣
可逆矩陣(2)設、是數域上的階矩陣,。
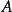 可逆矩陣
可逆矩陣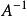 可逆矩陣
可逆矩陣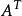 可逆矩陣
可逆矩陣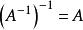 可逆矩陣
可逆矩陣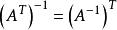 可逆矩陣
可逆矩陣①若可逆,則和也可逆,且,;
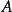 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣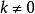 可逆矩陣
可逆矩陣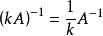 可逆矩陣
可逆矩陣②若可逆,則可逆,且;
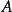 可逆矩陣
可逆矩陣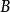 可逆矩陣
可逆矩陣 可逆矩陣
可逆矩陣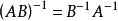 可逆矩陣
可逆矩陣③、均可逆。
常用方法
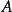 可逆矩陣
可逆矩陣(1)判斷或證明 可逆的常用方法:
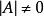 可逆矩陣
可逆矩陣①證明;
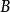 可逆矩陣
可逆矩陣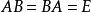 可逆矩陣
可逆矩陣②找一個同階矩陣,驗證;
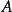 可逆矩陣
可逆矩陣③證明的行向量(或列向量)線性無關。
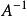 可逆矩陣
可逆矩陣(2)求 的方法:
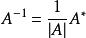 可逆矩陣
可逆矩陣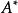 可逆矩陣
可逆矩陣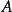 可逆矩陣
可逆矩陣①公式法:,其中為矩陣的伴隨矩陣。
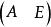 可逆矩陣
可逆矩陣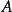 可逆矩陣
可逆矩陣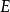 可逆矩陣
可逆矩陣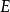 可逆矩陣
可逆矩陣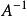 可逆矩陣
可逆矩陣②初等變換法:對作初等變換,將化為單位陣,單位矩陣就化為。