定義
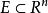 可測集
可測集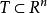 可測集
可測集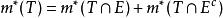 可測集
可測集設 ,若對任意的點集 ,有 ,則稱E為Lebesgue可測集,簡稱可測集。
注意事項如下:
(1)可測集的全體記為M,對於可測集E,稱其外測度為測度,記為m(E)。
(2)稱測度為零的可測集為零測集。空集、有限集、可數集皆為零測集。
(3)通常稱定義中的條件為卡氏條件,稱其中的集T為試驗集。
相關定理
零集
零集為可測集。
證明:設E為零集,m*(E)=0,任意A⊂R,因為A∩E⊂E,所以有0≤m*(A∩E)≤m*(E),得m*(A∩E)=0,於是
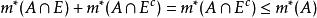 可測集
可測集故E∈M。
可測集的補集
若E為可測集,則E的補集也是可測集。
可測集的並集交集
若A,B為可測集,則A∪B,A∩B,A\B皆為可測集。
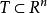 可測集
可測集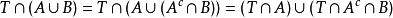 可測集
可測集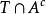 可測集
可測集證明:對任意 ,易得 ,依次利用外測度的次可加性、B的可測性(取 為試驗集)以及A的可測性(取T為試驗集),有:
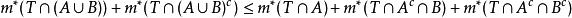 可測集
可測集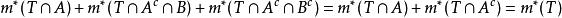 可測集
可測集且
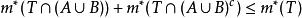 可測集
可測集故得到。
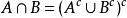 可測集
可測集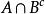 可測集
可測集所以可知A∪B是可測集,從而是可測集,A\B=也是可測集。
可數可加性
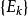 可測集
可測集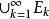 可測集
可測集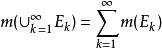 可測集
可測集若是互不相交的可測集列,則並集為可測集,且。
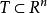 可測集
可測集證明:對任意的,由外測度的次可加性等性質可知
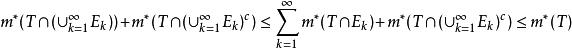 可測集
可測集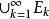 可測集
可測集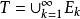 可測集
可測集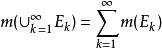 可測集
可測集所以是可測集,令,則有。
可測集列的交與並
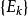 可測集
可測集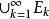 可測集
可測集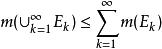 可測集
可測集(1)若是可測集列,則並集為可測集,且。
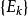 可測集
可測集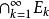 可測集
可測集(2)若是可測集列,則交集為可測集。
 可測集
可測集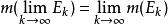 可測集
可測集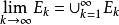 可測集
可測集(3)若有遞增可測集列,則,此時對可測集的極限有定義。
 可測集
可測集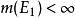 可測集
可測集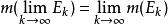 可測集
可測集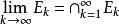 可測集
可測集(4)若有遞減可測集列,且,則,此時對可測集的極限有定義。
(5)任一可測集均可以表示為一列遞增的有界可測集之並。
(6)任一可測集均可以表示為一列兩兩不交的有界可測集之並。
可測集類
第一類
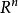 可測集
可測集中的矩體是可測集。
 可測集
可測集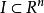 可測集
可測集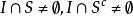 可測集
可測集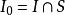 可測集
可測集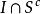 可測集
可測集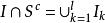 可測集
可測集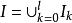 可測集
可測集證明:設矩體,對任意矩體,不妨設。記矩體,把分割成有限個互不相交的矩體之並:,則有,從而得到
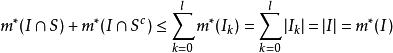 可測集
可測集此時易得,矩體S為可測集。
第二類
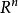 可測集
可測集由中開集的構造可知,每個開集可寫成可列個互不相交的半開半閉的矩體之並,故開集必為可測的。由此易得到如下結論:
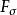 可測集
可測集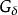 可測集
可測集開集、閉集、集、集、Borel集皆為可測集。
可測集的等價刻畫
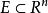 可測集
可測集設,則下列條件等價:
(1)E是可測集;
(2)對任意ε>0,存在開集G⊃E,使m*(G\E)<ε;
(3)對任意ε>0,存在閉集F⊂E,使m*(E\F)<ε;
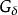 可測集
可測集(4)存在集H⊃E,使得m(H\E)=0;
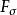 可測集
可測集(5)存在集K⊂E,使得m(E\K)=0。

