凸圖形

凸圖形在代數中的地位很重要，主要體現在它的分析或代數性質，並且已被套用到諸如數理經濟學等領域。凸形的幾何性質研究比較落後，也最為複雜。本詞條將就其定義、判定、性質作一些討論。

定義

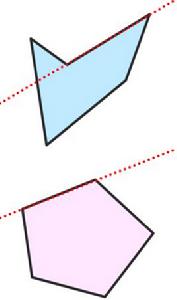
一個圖形F，對在F內的任意兩個點A、B，若線段AB上的所有點恆在圖形F內，則稱該圖形F為凸圖形。

否則稱之為非凸圖形。

註：這裡的圖形F可以是平面圖形、空間圖形等。

判定

凸圖形包括凸多邊形、凸多面體等。

1. 凸多邊形：延長多邊形的任意一邊為一條直線，若其餘的邊都在該直線同側，則稱之為凸多邊形。

2. 凸多面體：延展多面體的任意一面為一個平面，若其餘的面都在該平面同側，則稱之為凸多面體。

重要概念

直徑

這個概念適用於一般點集：有界點集中任意兩點距離的上確界（不一定能達到），若無上確界則為無窮大（幾乎沒有意義）。

支撐線

只與凸圖形在邊界上有公共點的直線。

每個平面凸集邊上的每一點至少有一條支撐線，把整個凸集分在平面的一側。

這是支撐線最重要的性質。