Hp 空間
正文
又稱哈代空間,勒貝格空間(lp)以外重要的函式空間之一。
單變數的hp空間,最早來源於複變函數論。設F(z)在複平面的單位圓D(|z|<1)內解析,量
化學表達式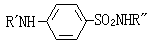 (1)刻畫了F 的模的p 次冪在圓周 |z|=r上的平均值的大小。假如它對0<r<1有界,其中0<p<∞,則稱F是屬於hp(D)的。當p≥1時,用μp(F,r)在0<r<1的上確界定義F 的hp 模,即
(1)刻畫了F 的模的p 次冪在圓周 |z|=r上的平均值的大小。假如它對0<r<1有界,其中0<p<∞,則稱F是屬於hp(D)的。當p≥1時,用μp(F,r)在0<r<1的上確界定義F 的hp 模,即
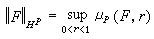 ,
,
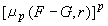 的上確界定義F 與G 的距離,即
的上確界定義F 與G 的距離,即 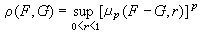 ,
,
可以證明,當F∈hp(D)(0<p<∞) 時,F(z)在單位圓周上的邊值幾乎處處存在,即
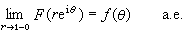 。
。
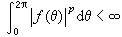 。 (2)
。 (2)
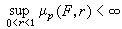
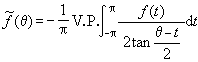 。
。
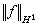 的大小與
的大小與 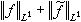 的大小是差不多的。歷史上,1915年英國數學家G.H.哈代引入了hp函式類,1923年匈牙利數學家F.(F.)里斯證明它們是完備的賦范空間或度量空間,並命名它們為哈代空間或簡稱hp空間。
的大小是差不多的。歷史上,1915年英國數學家G.H.哈代引入了hp函式類,1923年匈牙利數學家F.(F.)里斯證明它們是完備的賦范空間或度量空間,並命名它們為哈代空間或簡稱hp空間。 對於上半平面
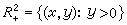 內的解析函式F(z),其中z=x+iy,可以類似地用
內的解析函式F(z),其中z=x+iy,可以類似地用 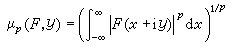
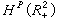 。這時它們的邊值
。這時它們的邊值 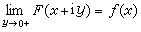
在傅立葉分析中,有很多定理對lp(p>1)成立,對l1並不成立,但對h1, 相應的結果卻是對的。典型的例子是哈代-李特爾伍德定理:如果ƒ∈lp(T)(1<p≤2)是周期函式,它的傅立葉級數是
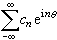 ,則
,則 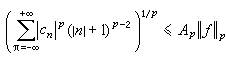 。
。
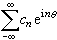 ,則定理的結果對p=1成立,即
,則定理的結果對p=1成立,即 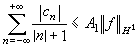 。
。
多變數hp空間的建立卻要晚得多,這是因為單元hp空間的定義緊密依賴於單元解析函式,然而形式地通過多元解析函式來定義多元hp空間,由於多元解析函式較單元解析函式複雜得多,未能得到預期的結果,因此需要尋求另外的辦法。1960年E.M.施坦和G.韋斯把上半平面的解析函式的實部與虛部的概念推廣到 n+1維歐氏空間的上半空間
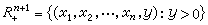 ,得到共軛調和函式系的概念。在
,得到共軛調和函式系的概念。在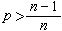 的前提下,定義了
的前提下,定義了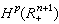 。與上半平面的情形相類似,共軛調和函式系在y→0+時的邊值函式構成hp(Rn)。1964年A.P.考爾德倫與A.贊格蒙把
。與上半平面的情形相類似,共軛調和函式系在y→0+時的邊值函式構成hp(Rn)。1964年A.P.考爾德倫與A.贊格蒙把 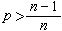 的條件改進為p>0,但形式上十分複雜。把hp(R)了解為hp(R崹)的廣義函式意義的邊值, 1970年D.L.伯克霍爾德、R.F.岡迪與M.L.西爾弗斯坦證明了廣義函式ƒ是hp(R)(p>0)中某個元素的實部的充分必要條件是極大函式
的條件改進為p>0,但形式上十分複雜。把hp(R)了解為hp(R崹)的廣義函式意義的邊值, 1970年D.L.伯克霍爾德、R.F.岡迪與M.L.西爾弗斯坦證明了廣義函式ƒ是hp(R)(p>0)中某個元素的實部的充分必要條件是極大函式 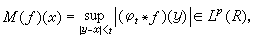 (3)
(3)
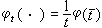 ,*表示卷積。1972年C.費弗曼和斯坦把這個結果推廣到了多元的情形。值得注意的是,M(ƒ∈lp這條件完全和解析函式的概念無關,它給出了hp空間的實變函式論特徵。這樣,就可以用類似於(3)的條件來定義 hp(Rn)本身而無須藉助任何解析函式或調和函式的概念了。
,*表示卷積。1972年C.費弗曼和斯坦把這個結果推廣到了多元的情形。值得注意的是,M(ƒ∈lp這條件完全和解析函式的概念無關,它給出了hp空間的實變函式論特徵。這樣,就可以用類似於(3)的條件來定義 hp(Rn)本身而無須藉助任何解析函式或調和函式的概念了。 1972年費弗曼和施坦還證明了,h1(Rn) 的對偶空間是BMO 空間。h1和BMO對偶關係的發現,使人們對這兩個空間的認識深入了一大步。它們已經成了Lp(Rn)(1≤p≤∞)空間理論的必不可少的補充。
近年來,數學家還找到了hp空間的許多其他特徵,使hp空間有許多的推廣。傅立葉分析、複分析、泛函分析以及偏微分方程的許多問題,都是在hp空間與BMO空間中進行討論的。此外,hp空間和BMO空間理論也進入到了機率論的鞅論中。
