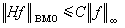BMO 空間

BMO 空間

正文

有界平均振動空間的簡稱。這是 1961年由 ƒ.約翰和L.尼倫伯格在研究橢圓型偏微分方程的解時所引進的一類函式空間。 它包含著空間L∞（Rn）,又是哈代空間H1（Rn）的對偶空間 （見Hp 空間）。設ƒ（x）為定義於Rn上的局部可積函式，Q為Rn中邊平行坐標軸的任一立方體，│Q│為其體積,ƒ（x）同ƒ(x)在Q上的平均值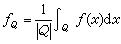的偏差用│ƒ(x)-ƒQ│表示, 它在Q上的平均值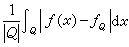，叫做ƒ(x)在Q上的平均振幅。如果ƒ(x)滿足條件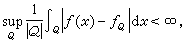

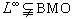就稱ƒ(x)具有有界的平均振幅，並記作ƒ∈BMO。由上述定義看出，任一Rn上的有界可測函式必具有有界的平均振幅,但反之不一定成立。例如，log｜x｜屬於BMO空間,但它不屬於L∞，這說明 BMO空間和L∞有嚴格的包含關係。
BMO空間與巴拿赫空間　對任一ƒ∈BMO，如定義

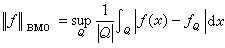
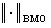,可以證明為一準範數。事實上,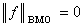若且唯若ƒ(x)為一常數。因此,當BMO空間中的兩個函式ƒ1和ƒ2相差一常數時，規定這兩個函式是等同的，在這個規定之下,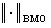便成為範數,而且BMO空間為一巴拿赫空間。
約翰－尼倫伯格不等式　由 BMO空間的定義容易驗證：如果存在兩正常數A和α,使得對於一切的立方體Q均滿足

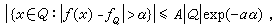
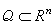式中左邊為勒貝格測度，那么ƒ∈BMO。約翰和尼倫伯格指出上述不等式本質上可以用來刻畫BMO空間的特徵。這就是存在著兩正常數A和α,使得對於任一ƒ∈BMO,立方體，以及α>0，成立不等式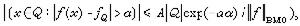

費弗曼－施坦分解 另一個涉及BMO空間構造特徵是由 C.L.費弗曼和 E.M.施坦給出的：ƒ∈BMO若且唯若ƒ=u+堝，此處u,υ∈L∞,堝為υ的希爾伯特變換。這個事實表明,判斷一個函式是否屬於BMO空間，可以純粹用調和分析的語言來表述與刻畫。因此，這個事實也就成為揭示BMO空間和調和分析之間內在關係的紐帶,並且這方面的進一步研究成為當代調和分析的重要研究課題之一。
費弗曼－施坦定理　關於BMO空間的研究,特別要提出費弗曼和施坦的下述結果:哈代空間H1(Rn)的對偶空間為BMO空間，記作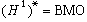。可以說，由於這個事實的發現，BMO空間便成為調和分析的重要角色。
套用　由於BMO空間是H1的對偶空間,因此許多涉及H1的問題通過這個對偶關係可以用 BMO空間的性質去處理，於是BMO空間就成為研究 H1許多問題的一個新工具。例如，研究運算元T從H1到L1的有界性，要建立不等式

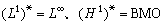(*)由以及關係式

可知：

。

於是，為使關係式(*)成立，只須證明

。

這就把研究運算元從H1到L1的有界性問題轉化為研究其共軛運算元慘從L∞到BMO空間的有界性問題了。另一個套用是，BMO空間在許多調和分析問題的研究中,可以成為空間L∞的合適代替。例如,傅立葉分析中的許多古典的運算元T具有從Lp到Lp的有界性(1<p<∞)，也就是說不等式

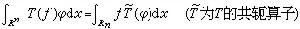
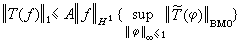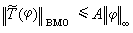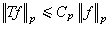
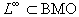成立。但當p=∞時,結論卻不成立。其原因是由於當ƒ∈L∞時,經過運算元T作用後的像Tƒ不一定在L∞內。包含關係使人們想到，映像Tƒ雖不在L∞內，但有可能在BMO空間內,如果這是正確的話,說明運算元T有可能具有從L∞到BMO空間的有界性。例如希爾伯特變換H雖不滿足

,

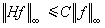但成立著

。因此，當運算元T並不具有從L∞到L∞的有界性時,可以考慮T是否具有從L∞到BMO空間的有界性。在這種意義下,BMO空間起到了代替L∞的作用。

配圖

相關連線