簡介
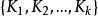 類方程
類方程 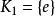 類方程
類方程 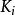 類方程
類方程 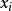 類方程
類方程 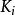 類方程
類方程 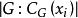 類方程
類方程 設 G 為有限群,群 G 的元素按共軛關係分成一個個共軛類。設是 G 的全部共軛類。習慣上。在每個共軛類中取一個代表元,於是共軛類的長度為。進而有
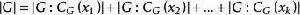 類方程
類方程 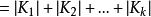 類方程
類方程 上面的等式稱為 G 的類方程。
共軛
互為共軛的子集在同一軌道里,這個軌道一般叫做 共軛類,共軛類中的元素互為共軛。子集S的穩定子滿足gSg =S,它也稱為S的 正規化子,記作N(S),它是一個子群。這樣一來,共軛類的中的元素和N(S)的陪集一一對應,每個共軛類中有[G:N(S)]個元素。進一步地,共軛類中每個元素的正規化子有N(gSg )=gN(S)g ,它們也形成一個共軛類。
首先,以上X中可以只取那些只有一個元素的子集,這個情況等價於X=G,這就相當於定義了群元素間的共軛關係。群的元素在共軛的作用下分成了多個等價類,而不動元素FG顯然就是中心C。如果中心元有c個,其它等價類C分別有c個元素(k=1,2,⋯,m),則類方程變成:G=C∪C∪C∪⋯∪C,|G|=c+c+c+⋯+c
其次,還可以把X中的元素限定為子群,這就定義了 共軛子群。共軛子群具有共軛子集一樣的性質,只是在子集和其正規化子的關係上有本質不同。對一般子集,不一定有S⊆N(S),而對於子群H不僅有H⊆N(H),還有H⊴N(H)。從另一個角度看,N(H)其實是通過縮小G來使H成為正規子群,N(H)是G中使H稱為正規子群的最大子群。考察H的所有共軛子群之交K=∩H,可以證明aHa 任然包含所有H的共軛子群,從而恆有aKa =K,即K為正規子群。特別的,如果H的指數有限,則K的指數也有限。
相對於單個元素的正規化子,子集的正規化子其實是被弱化的。正規化子N(x)是所有滿足axa =x的元素,即所有與x可交換的元素。為此可以定義與子集S所有元素可交換的集合,稱它為S的 中心化子,並記做C(S)。容易證明它也是子群,並且有C(S)⊴N(S)成立。而對單個元素顯然有:C(x)=N(x)。

