定義
在直角坐標系中一條連續曲線L的參數方程為
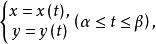 連續曲線
連續曲線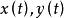 連續曲線
連續曲線此處是實連續函式,那么在複平面上,連續曲線L就可以表示為
 連續曲線
連續曲線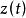 連續曲線
連續曲線此處是實變數的復連續函式 。
相關性質
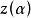 連續曲線
連續曲線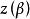 連續曲線
連續曲線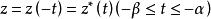 連續曲線
連續曲線指定了起點和終點的連續曲線稱為 有向曲線,若不作特別說明,一般規定沿參數 t 增加的方向為 曲線正方向,即連續曲線(1)以為起點,而以為終點,這時(1)的反向曲線可表作。
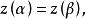 連續曲線
連續曲線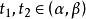 連續曲線
連續曲線若即L的兩個端點重合,則稱L為 閉曲線。若有,使得z(t)=z(t),它們就是曲線L上的 重點,沒有重點的曲線稱為 簡單曲線,僅僅在兩個端點重合的曲線稱為 簡單閉曲線。
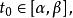 連續曲線
連續曲線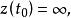 連續曲線
連續曲線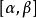 連續曲線
連續曲線若有使得而z(t)是上的廣義連續函式,則稱L為 廣義連續曲線。例如,射線為廣義簡單曲線;直線為廣義簡單閉曲線。
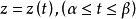 連續曲線
連續曲線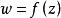 連續曲線
連續曲線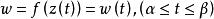 連續曲線
連續曲線連續曲線經連續函式映照的象仍是一條連續曲線,它的參數表示為。
一條簡單閉曲線L將平面分為兩個沒有交集的區域,它們以L為公共邊界,其中一個為有界的區域,稱為 內部;另一個為無界的區域,稱為 外部。這是著名的 約當定理。
以上結論對擴充複平面上的廣義簡單閉曲線也是正確的,只是被它分成的兩個區域將都是無界的。
如果一個區域的邊界為簡單閉曲線,則規定邊界曲線(相對於區域的)正方向為:當沿邊界曲線正方向行進時,區域應保持在其左方。
擴充複平面上的一個區域D稱為 單連通區域,若屬於D的任意一條簡單閉曲線的內部或外部之一仍屬於D,否則就稱為 多連通區域。複平面及擴充複平面本身就都是單連通區域。
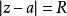 連續曲線
連續曲線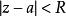 連續曲線
連續曲線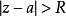 連續曲線
連續曲線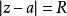 連續曲線
連續曲線 連續曲線
連續曲線例如,圓周將擴充複平面分為兩個區域,圓內及圓外,它們都是單連通區域,它們以圓周為公共邊界。顯然,對於不包含點的複平面,圓外不再是單連通區域,而是一個無界的多連通區域。
從擴充複平面上除去一條非閉的簡單曲線L,餘下的部分是一個單連通區域,這樣的非閉的簡單曲線L形象地稱為 割口,所得的區域稱為 帶割口的區域,割口上的點(非端點)看作是重疊在一起的分別屬於割口兩側的兩個邊界點。
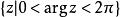 連續曲線
連續曲線例如沿正半實軸割開的複平面:就是一個帶割口的區域;沿著區間[一1,1]割開的擴充複平面也是一個帶割口的區域。
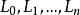 連續曲線
連續曲線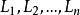 連續曲線
連續曲線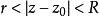 連續曲線
連續曲線 連續曲線
連續曲線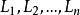 連續曲線
連續曲線設是複平面上n+1條簡單閉曲線,其中這n條曲線互不相交且互不包含另一條曲線在其內部,但它們全在L的內部,則稱以這n+1條簡單閉曲線為邊界的區域為n+1 連通區域。特別地,上述的n+1條簡單閉曲線都允許其中任意一條退化為一段制口,甚至是一個孤立點,例如圓環及鄰環都是有界的二連通區域;再如,若L退化為點,那得到的將是擴充複平面上的無界的n+1連通區域;若L不存在,那么,以這n條曲線為邊界的區域就是擴充複平面上的無界的n連通區域 。

