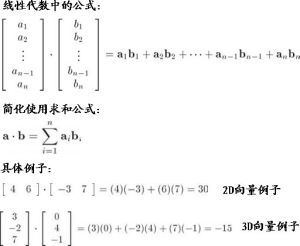
點乘的值
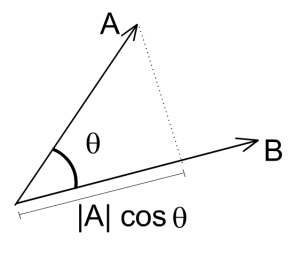 點積
點積 兩個單位向量的點積得到兩個向量的夾角的cos值,通過它可以知道兩個向量的相似性,利用點積可判斷一個多邊形是否面向攝像機還是背向攝像機。
向量的點積與它們夾角的餘弦成正比,因此在聚光燈的效果計算中,可以根據點積來得到光照效果,如果點積越大,說明夾角越小,則物理離光照的軸線越近,光照越強。
運算律
1.交換律:α·β=β·α 2.分配律:(α+β)·γ=α·γ+β·γ 3.若λ為數:(λα)·β=λ(α·β)=α·(λβ) 若λ、μ為數::(λα)·(μβ)=λμ(α·β) 4.α·α=|α|² ,此外:α·α=0〈=〉α=0。 向量的數量積不滿足消去律,即一般情況下:α·β=α·γ,α≠0 ≠〉β=γ。 向量的數量積不滿足結合律,即一般(α·β)·γ ≠〉α·(β·γ) 相互垂直的兩向量數量積為0
坐標表示
已知兩個非零向量a=(x1,y1),b=(x2,y2),則有a·b=x1x2+y1y2,即兩個向量的數量積等於它們對應坐標的乘積的和。套用
平面向量的數量積a·b是一個非常重要的概念,利用它可以很容易地證明平面幾何的許多命題,例如勾股定理、菱形的對角線相互垂直、矩形的對角線相等等。如證明:(1)勾股定理: Rt△ABC中,∠C=90°,則|CA|^2+|CB|^2=|AB|^2。
∵AB = CB-CA
∴AB·AB =(CB-CA)·(CB-CA)= CB·CB-2CA·CB+CA·CA
又∵ ∠C=90°,有CA⊥CB,於是CA·CB=0
∴ AB·AB=AC·AC+CB·CB
(2)菱形對角線相互垂直: 菱形ABCD中,點O為對角線AC、BD的交點,求證AC⊥BD。
設 |AB|=|BC|=|CD|=|DA|=a
∵AC=(AB+BC)cosα,BD=(BC+CD)cos(π-α)
∴AC·BD=(AB+BC)cosα·(BC+CD)cos(π-α)=a^2(cosα+cos(π-α)+1-1 )
又∵ cosα=-cos(π-α)
∴AC·BD=(AB+BC)cosα·(BC+CD)cos(π-α)=a^2(cosα+cos(π-α)+1-1 )=0
∴AC⊥BD
在生產生活中,點積同樣套用廣泛。利用點積可判斷一個多邊形是否面向攝像機還是背向攝像機。向量的點積與它們夾角的餘弦成正比,因此在聚光燈的效果計算中,可以根據點積來得到光照效果,如果點積越大,說明夾角越小,則物理離光照的軸線越近,光照越。物理中,點積可以用來計算合力和功。若b為單位矢量,則點積即為a在方向b的投影,即給出了力在這個方向上的分解。功即是力和位移的點積。計算機圖形學常用來進行方向性判斷,如兩矢量點積大於0,則它們的方向朝向相近;如果小於0,則方向相反。矢量內積是人工智慧領域中的神經網路技術的數學基礎之一,此方法還被用於動畫渲染(Animation-Rendering)。
線性變換中點積的意義:
根據點積的代數公式:a·b=a1b1+a2b2+……+anbn,假設a為給定權重向量,b為特徵向量,則a·b其實為一種線性組合,函式F(a·b)則可以構建一個基於a·b+c = 0 (c為偏移)的某一超平面的線性分類器,F是個簡單函式,會將超過一定閾值的值對應到第一類,其它的值對應到第二類。