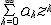定義
整函式總可以在原點展開成泰勒級數,它在全平面收斂,整函式以∞點為唯一的孤立奇點,它在∞點的羅朗展式與它在原點的泰勒展式有一樣的形式。當∞點是整函式的可去奇點時,這個整函式只能是常數,這就是著名的劉維爾定理,通常表述為“有界整函式必為常數”。
劉維爾定理
劉維爾(Liouville)定理
若f(z)在全平面C上全純且有界,則f為常數。
證明
若|f(z)|≤M,當z∈C。固定a∈C,作D(a,R),由柯西不等式得到|f`(a)|≤M/R。令R→∞,得到f`(a)=0。由於a為C中任意一點,故f`(z)=0對任意z∈C都成立,因此f(z)在C上為常數。
簡單證明
利用這一定理可以得到代數基本定理的簡單證明。當∞點是整函式的n階極點時,這個整函式是一個n次多項式 ,也就是它的泰勒展式(或羅朗展式)只有有限多項。當∞點是整函式的本性奇點時,這個整函式的泰勒展式一定有無限多項,這類整函式稱為超越整函式。由代數基本定理知道n次多項式一定有n個零點(也就是根),它總可以分解為n個一次因式的積,對於超越整函式,它可能有無限多個零點 ,比如sinπz就以全體整數為其零點集,也有的超越整函式沒有零點,如ez就處處不為零,一般來說,沒有零點的超越整函式總可以表成eg(z)的形式,此處g(z)也是一個整函式,而有無限多個零點的超越整函式f(z)也有一個因子分解式 ;形如 ,其中g(z)是整函式,0是m階零點,zk是非零零點集,gk()是的多項式,這是魏爾斯托拉斯因子分解定理。超越整函式還有一個重要性質:若f(z)是超越整函式,則對任意複數A(包括A=∞),存在點列{zk },使zk ∞(k∞)而有f(zk)A。
這一結果有一個更精確的發展:對超越整函式f(z),最多除去一個值(稱為例外值)外,對所有其他的複數v值(v≠∞),f(z)-v都有無窮多個零點(畢卡定理)。