契比雪夫不等式

契比雪夫不等式實質上是排序不等式的一個推廣。在除數學之外的其他領域也有廣泛套用。

證明概念

對於n個正數a1~an以及b1~bn,有排序關係，有

若a1≤a2≤···≤an，b1≤b2≤···≤bn，則

a1bn+a2b(n-1)+···+anb1≤（1/n）*（a1+a2+···+an)(b1+b2+···+bn)≤a1b1+a2b2+···+anbn，

若且唯若a1=a2=···=an，或b1=b2=···=bn時，等號成立。

該不等式即為契比雪夫(chebyshev)不等式。

證明過程

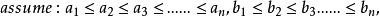契比雪夫不等式

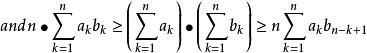契比雪夫不等式

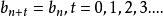契比雪夫不等式

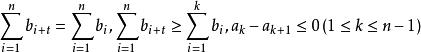契比雪夫不等式

Proof :定義則

由分部求和公式，

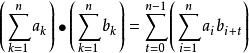契比雪夫不等式

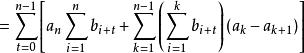契比雪夫不等式

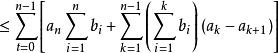契比雪夫不等式

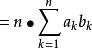契比雪夫不等式

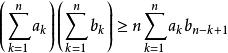契比雪夫不等式

同理可證