說明
排序不等式表述如下，設有兩組數a,a,……a和b,b,……b滿足a≤a≤……≤a,b≤b≤……≤b，c,c,……c是b,b,……b的亂序排列，則有ab+ab+……+ab≤ac+ac+……+ac≤ab+ab+ab,若且唯若a=a=……=a或b=b=……=b時等號成立。一般為了便於記憶，常記為：反序和≤亂序和≤順序和.
套用
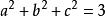排序不等式設a,b,c≥0 ,則ab+bc+ca的最大值為_______.
【解題指南】由於a,b,c的地位是均等的，不妨設a≥b≥c≥0，然後利用排序不等式求解.
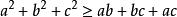排序不等式【解析】由排序不等式 ，得ab+bc+ca≤3.即ab+bc+ca的最大值為3.
答案：3
排序不等式的證明
①分析法
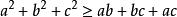排序不等式要證
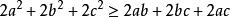排序不等式只需證
排序不等式只需證
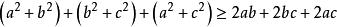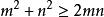排序不等式根據基本不等式
∴原結論正確
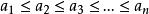排序不等式
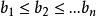排序不等式②設有兩個有序數組： 及
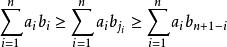排序不等式求證： (順序和≥亂序和≥逆序和)
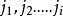排序不等式其中 是自然數的任何一個排列
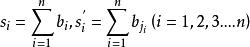排序不等式證明：令
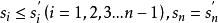排序不等式由題設易知
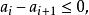排序不等式
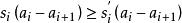排序不等式因為 故
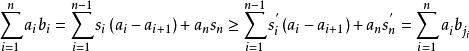排序不等式所以
即左端不等式，類似可證明右端不等式
