定義
 垂足曲線
垂足曲線 垂足曲線
垂足曲線 垂足曲線
垂足曲線 垂足曲線
垂足曲線在平面內,過定點O向曲線 的切線作垂線,其垂足的軌跡就叫做曲線 關於點 的 垂足曲線。例如,圓關於任意點的垂足曲線是蝸線;拋物線關於其焦點的垂足曲線是直線;等軸雙曲線關於其中心的垂足曲線是雙紐線。曲線 對於其垂足曲線叫做 反垂足曲線 。
垂足曲線的方程
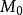 垂足曲線
垂足曲線 垂足曲線
垂足曲線 垂足曲線
垂足曲線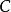 垂足曲線
垂足曲線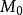 垂足曲線
垂足曲線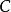 垂足曲線
垂足曲線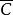 垂足曲線
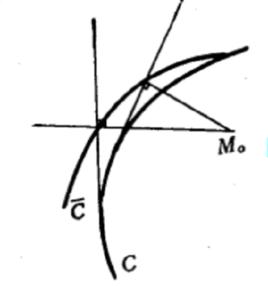
垂足曲線我們稱定點 對曲線 上各點切線作垂線的垂足所形成的曲線 ,為曲線 對 點的垂足曲線,而稱曲線 為曲線 的反垂足曲線。如圖1所示 。
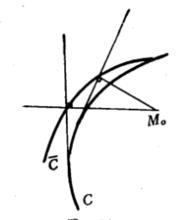 圖1
圖1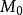 垂足曲線
垂足曲線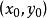 垂足曲線
垂足曲線若設 點的坐標為 ,曲線C的方程為
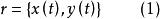 垂足曲線
垂足曲線則其上任一點的切線方程為
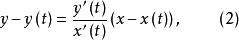 垂足曲線
垂足曲線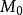 垂足曲線
垂足曲線過 點與此切線垂直的直線方程為
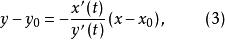 垂足曲線
垂足曲線 垂足曲線
垂足曲線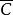 垂足曲線
垂足曲線垂足為方程(2)和(3) 所示直線的交點。當 連續變化時,方程(2)和(3)的聯立解即為垂足曲線 的方程。 即:
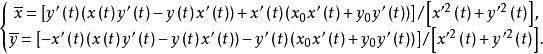 垂足曲線
垂足曲線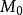 垂足曲線
垂足曲線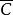 垂足曲線
垂足曲線反垂足曲線是垂足曲線上點與 連線(徑向線) 的垂線族的包絡。現在極坐標系下由已知垂足曲線 的方程
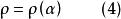 垂足曲線
垂足曲線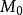 垂足曲線
垂足曲線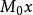 垂足曲線
垂足曲線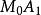 垂足曲線
垂足曲線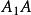 垂足曲線
垂足曲線推導反垂足曲線C的方程。為便於分析起見,現約定方程:(4)為取 為極點,極軸為圖2中 的特定條件下的表達式。見圖2,極徑 的垂線 的方程為
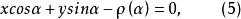 垂足曲線
垂足曲線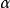 垂足曲線
垂足曲線這是單參數 的直線族。C為其包絡則必須滿足
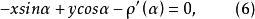 垂足曲線
垂足曲線於是聯立式(5)、(6)兩式,可得反垂足曲線C的方程
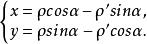 垂足曲線
垂足曲線由上式可知
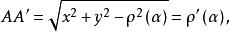 垂足曲線
垂足曲線還可以推出曲線C的曲率半徑為
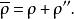 垂足曲線
垂足曲線