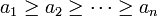形式
它可以比較兩組數積的和及兩組數的線性和的積的大小：
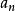切比雪夫總和不等式
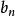切比雪夫總和不等式對於兩個實數數列{ }、{ }
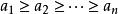切比雪夫總和不等式
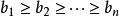切比雪夫總和不等式若有 ，
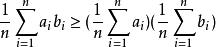切比雪夫總和不等式則有
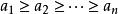切比雪夫總和不等式
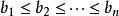切比雪夫總和不等式類似的，若有 ，
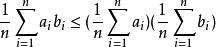切比雪夫總和不等式則有
證明
證明一
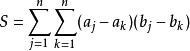切比雪夫總和不等式考慮和式：
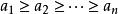切比雪夫總和不等式 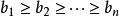切比雪夫總和不等式
切比雪夫總和不等式因為有 ， ，所以顯然有
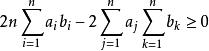切比雪夫總和不等式將其展開可得
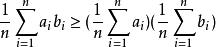切比雪夫總和不等式整理可得
反向情況類似，得證。
證明二
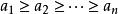切比雪夫總和不等式 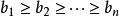切比雪夫總和不等式因為有 ，
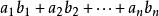切比雪夫總和不等式所以由排序不等式易知，最大的和為順序和，即：
於是有以下一系列共 n個不等式：
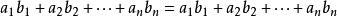切比雪夫總和不等式
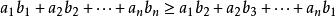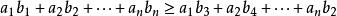切比雪夫總和不等式
切比雪夫總和不等式
切比雪夫總和不等式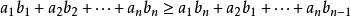
切比雪夫總和不等式將這 n 個不等式分別相加，同時對右式進行因式分解，整理可得：
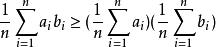切比雪夫總和不等式反向情況可由最小的和為逆序和推得，得證。
積分形式
切比雪夫總和不等式
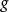切比雪夫總和不等式如果 、 是在[0,1]上的可積實值函式，並且它們同時單增或單減，那么有：
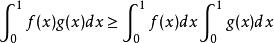切比雪夫總和不等式 切比雪夫總和不等式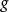 切比雪夫總和不等式類似的，若
、一個單增一個單減，那么有：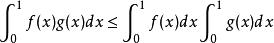
切比雪夫總和不等式