定義
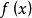 一致連續
一致連續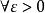 一致連續
一致連續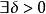 一致連續
一致連續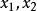 一致連續
一致連續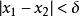 一致連續
一致連續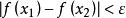 一致連續
一致連續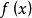 一致連續
一致連續設函式在區間I上有定義,如果,,使得對於在區間I上的任意兩點,當時,恆有,則稱函式在區間I上一致連續。
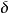 一致連續
一致連續 一致連續
一致連續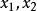 一致連續
一致連續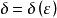 一致連續
一致連續參數僅與有關,與所選取的任意兩點無關,即。
意義
從上述定義中可以看出,當函式在區間I上一致連續時,無論在區間I上的任何部分,只要自變數的兩個數值接近到一定程度,總可以使相應的函式值達到預先指定的接近程度。
定理
定理1 Cantor定理或一致連續性定理
 一致連續
一致連續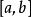 一致連續
一致連續 一致連續
一致連續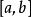 一致連續
一致連續若函式在上連續,則在上一致連續。
定理2
 一致連續
一致連續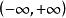 一致連續
一致連續 一致連續
一致連續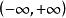 一致連續
一致連續若函式為上的連續周期函式,則在上一致連續。
定理3
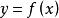 一致連續
一致連續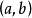 一致連續
一致連續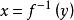 一致連續
一致連續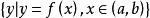 一致連續
一致連續若在有限開區間上嚴格單調且連續,則其反函式在區間上一致連續。
定理4
 一致連續
一致連續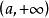 一致連續
一致連續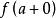 一致連續
一致連續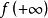 一致連續
一致連續 一致連續
一致連續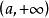 一致連續
一致連續設在上連續,若和都存在,則在上一致連續。
定理5
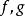 一致連續
一致連續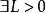 一致連續
一致連續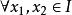 一致連續
一致連續設對於定義在區間I上的函式,,,有
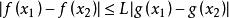 一致連續
一致連續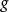 一致連續
一致連續 一致連續
一致連續成立,若在I上一致連續,則在I上也一致連續。
性質
 一致連續
一致連續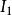 一致連續
一致連續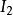 一致連續
一致連續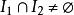 一致連續
一致連續 一致連續
一致連續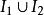 一致連續
一致連續1)設函式 在區間 和 上一致連續,若 ,則 在 上也一致連續;
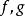 一致連續
一致連續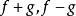 一致連續
一致連續2)若函式 都在區間I上一致連續,則 也在區間I上一致連續;
 一致連續
一致連續 一致連續
一致連續3)若 在有限區間I上一致連續,則 在I上有界;
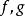 一致連續
一致連續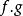 一致連續
一致連續4)若函式 都在有限區間I上的有界的一致連續函式,則在區間I上也一致連續;
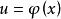 一致連續
一致連續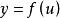 一致連續
一致連續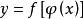 一致連續
一致連續5)若在定義域I上一致連續,其值域為U,在U上一致連續,則在I上一致連續。
舉例
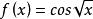 一致連續
一致連續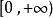 一致連續
一致連續函式在上一致連續。
證明如下:
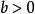 一致連續
一致連續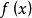 一致連續
一致連續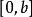 一致連續
一致連續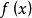 一致連續
一致連續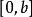 一致連續
一致連續①任取,由三角函式可知在閉區間上連續,由上述的定理1可知,在上一致連續。
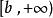 一致連續
一致連續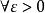 一致連續
一致連續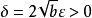 一致連續
一致連續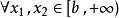 一致連續
一致連續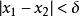 一致連續
一致連續②對於區間,對,取,對,當時,有
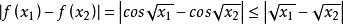 一致連續
一致連續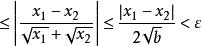 一致連續
一致連續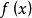 一致連續
一致連續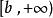 一致連續
一致連續即在區間上一致連續。
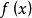 一致連續
一致連續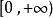 一致連續
一致連續綜上,在上一致連續。

