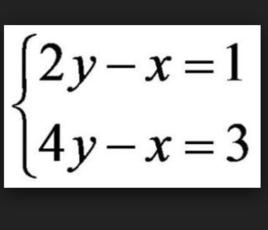定義
一次方程式也被稱為線性方程,因為在笛卡爾坐標繫上任何一個一次方程的表示都是一條直線。組成一次方程的每個項必須是常數或者是一個常數和一個變數的乘積。且方程中必須包含一個變數,因為如果沒有變數只有常數的式子是代數式而非方程式。
如果一個一次方程中只包含一個變數(x),那么該方程就是一元一次方程。如果包含兩個變數(x和y),那么就是一個二元一次方程,以此類推。
一元一次方程
一元一次方程式是指一個方程式中僅含有一個變數,且等號兩邊至少有一個一次單項式的方程。
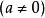 一次方程
一次方程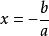 一次方程
一次方程任意一個一元一次方程形式經化 的方程。它的解為 以下就是一個例子:
x-17=-17x+3.
它的解便是:
20x=20.
x=1.
一元一次方程式是等於一條線性方程式:簡單點來說,如 x 或以上的次方是不容許的。
注意:當a=0時
ax+b=0不是一元一次方程式。
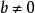 一次方程
一次方程如果 ,此方程式無限多解;如果 b=0,則此方程式恰一解。
二元一次方程
求解 二元一次聯立方程式可以使用代入消去法或加減消去法。
代入消去法
代入消去法就是先利用其中一個方程,將含有其中一個未知數的代數式表示另一個未知數。然後代入另一個方程,從而將這組方程轉化成解兩個一元一次方程式的方法。
例如:
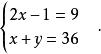 一次方程
一次方程解2x-1=9.
得x=5.
再代入x+y=36.
即5+y=36.
從而求出y=36-5=31.
加減消去法
加減消去法就是將兩個方程加或相減,從而消去其中一個未知數的方法。
通常,我們先將其中一個方程的兩邊同時乘以一個不是0的數,使其中的一個係數與另外一個方程的對應係數相同。再將兩個方程相加或相減。
例如:
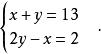 一次方程
一次方程把兩式相加消去x,即
y+2y=13+2.
從而求出
y=5.
線性化
通常 線性方程在實際套用中寫作:
•y=f(x).
這裡 f有如下特性:
•f(x+y)=f(x)+f(y).
•f(ax)=af(x).
這裡 a不是向量。
一個函式如果滿足這樣的特性就叫做 線性函式,或者更一般的,叫線性化。
因為線性的獨特屬性,在同類方程中對線性函式的解決有疊加作用。這使得線性方程最容易解決和推演。
線性方程在套用數學中有重要規律。使用它們建立模型很容易,而且在某些情況下可以假設變數的變動非常小,這樣許多非線性方程就轉化為線性方程。
微分
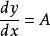 一次方程
一次方程若y=Ax+B,則 。
所以,線性函式並無駐點,即沒有極大值和極小值,且線性函式的斜率是未知數 x的係數。
相關條目
•二次方程
•直線–斜率
•一次不定方程
•微積分–微分–駐點–拐點
•格林函式