定義
假定以下材料:
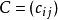Kac-Moody代數
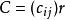Kac-Moody代數——一個r秩廣義嘉當矩陣(generalised Cartan matrix)
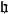Kac-Moody代數 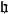Kac-Moody代數———— 一個 2n−r 維復向量空間
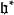Kac-Moody代數 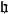Kac-Moody代數———— 的對偶空間
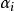Kac-Moody代數 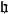Kac-Moody代數———— 中n枚相互線性獨立的元，稱為對偶根(co-root)
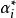Kac-Moody代數 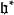Kac-Moody代數———— 中n枚線性相互線性獨立的元，稱為根(root)
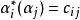Kac-Moody代數上述各元滿足
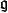Kac-Moody代數Kac–Moody代數
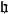Kac-Moody代數由符號 e, f (i=1,..,n) 及空間 生成：
以上各元滿足以下關係:
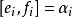Kac-Moody代數；
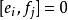Kac-Moody代數
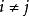Kac-Moody代數；其中 ；
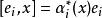Kac-Moody代數
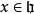Kac-Moody代數，其中 ；
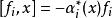Kac-Moody代數 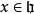Kac-Moody代數，其中 ；
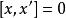Kac-Moody代數
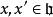Kac-Moody代數，其中 ；
，其中e出現1-c次；
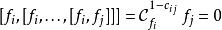Kac-Moody代數，其中f出現1-c 次。
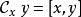Kac-Moody代數(其中 )
一個 實(維數可以無限)李代數亦可稱為Kac–Moody代數，如果復化是 Kac–Moody代數的話。
釋義
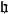Kac-Moody代數是此 Kac–Moody 代數的一嘉當子代數。
若g是 Kac–Moody 代數的一元，使得
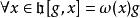Kac-Moody代數 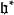Kac-Moody代數其中 ω 是 的一元，
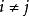Kac-Moody代數 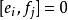Kac-Moody代數則稱g為權(weight) ω的。我們可分解一Kac–Moody 代數成其冪空間，則嘉當子代數的冪為零， e的冪為α*，而 f的冪為−α*。若二冪特徵向量的李括弧非零，則其冪是二冪之和。（若 ） 則 一條件即指 α* 都是簡單根。
