定義
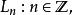 維拉宿代數
維拉宿代數維拉宿代數是一李代數,生成元是 c ,符合:
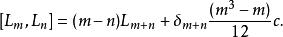 維拉宿代數
維拉宿代數推導
維拉宿代數可以被認為是以下Witt 代數的中心拓展:
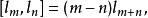 維拉宿代數
維拉宿代數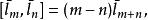 維拉宿代數
維拉宿代數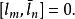 維拉宿代數
維拉宿代數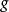 維拉宿代數
維拉宿代數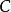 維拉宿代數
維拉宿代數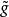 維拉宿代數
維拉宿代數對於一李代數 ,其在複數域 的central extension 滿足下列交換子:
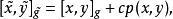 維拉宿代數
維拉宿代數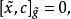 維拉宿代數
維拉宿代數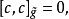 維拉宿代數
維拉宿代數其中
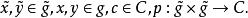 維拉宿代數
維拉宿代數由此定義, 維拉宿代數的生成元滿足以下交換子
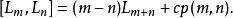 維拉宿代數
維拉宿代數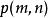 維拉宿代數
維拉宿代數可以由以下條件決定:
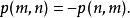 維拉宿代數
維拉宿代數交換子必須是反對易的, 所以
可以觀察到, 如果定義以下生成元
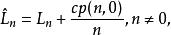 維拉宿代數
維拉宿代數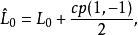 維拉宿代數
維拉宿代數它們滿足
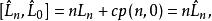 維拉宿代數
維拉宿代數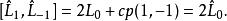 維拉宿代數
維拉宿代數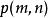 維拉宿代數
維拉宿代數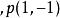 維拉宿代數
維拉宿代數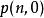 維拉宿代數
維拉宿代數比較函式 的定義可以得知 與 總是可以被設為0.
交換子滿足雅可比恆等式,即
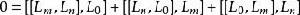 維拉宿代數
維拉宿代數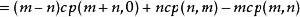 維拉宿代數
維拉宿代數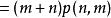 維拉宿代數
維拉宿代數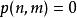 維拉宿代數
維拉宿代數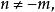 維拉宿代數
維拉宿代數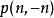 維拉宿代數
維拉宿代數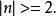 維拉宿代數
維拉宿代數所以 如果 即唯一的非零 central extension為 且
最後計算以下雅克比恆等式
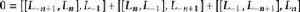 維拉宿代數
維拉宿代數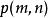 維拉宿代數
維拉宿代數可知 滿足以下遞推公式
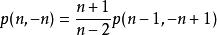 維拉宿代數
維拉宿代數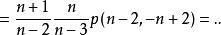 維拉宿代數
維拉宿代數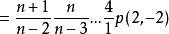 維拉宿代數
維拉宿代數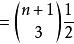 維拉宿代數
維拉宿代數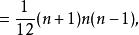 維拉宿代數
維拉宿代數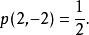 維拉宿代數
維拉宿代數其中歸一化條件為 綜上所述, Witt algebra在複數域唯一非零的central extension, 即維拉宿代數的生成元滿足以下交換子
 維拉宿代數
維拉宿代數