簡介
頂點代數(vertex algebra)又稱 頂點運算元代數(vertex operator algebra),是共形場論(保角場論)之代數結構。其套用包括怪獸月光理論(Monstrous moonshine)與幾何化朗蘭茲綱領。
1986 年,Richard Borcherds 受二維共形場論中用以插入場之頂點運算元啟發,提出頂點運算元代數結構。 重要例子有:
•晶格頂點運算元代數(用以研究晶格共形場論),
•來自仿射Kac-Moody 代數之表示之頂點運算元代數 (用以研究Wess-Zumino-Witten 模型),
•來自仿射Virasoro 代數之表示之Virasoro 頂點運算元代數 (可用以研究極小模型),
•I.Frenkel-J.Lepowsky-A/Meurman(於1988年)構造 之月光模(Moonshine module)V。
定義頂點運算元代數之各公理抽象自物理學人所謂之手征代數(Chiral algebra),其嚴格數學定義由 Beilinson 與 Drinfeld 提出。
定義
 頂點代數
頂點代數 頂點代數
頂點代數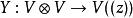 頂點代數
頂點代數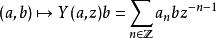 頂點代數
頂點代數一 頂點代數由以下資料組成:向量空間V,“單位元”1V,自態射T,乘法性映射: 或寫作 ;並滿足以下條件::
1.( 單位)V中每一元a,均符合
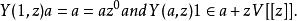 頂點代數
頂點代數2.( 位移)T(1) = 0, 且V中每元a,b, 均符合
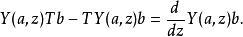 頂點代數
頂點代數3.( 四頂點函式)V中每元a,b,c, 均符合
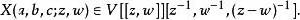 頂點代數
頂點代數其中Y(a,z)Y(b,w)c,Y(b,w)Y(a,z)c, 與Y(Y(a,z-w)b,w)c分別為X(a,b,c;z,w)在V((z))((w)),V((w))((z)), 與V((w))((z-w))中之級數展開式。
此乘法映射常被寫作“狀態—場 對應”(state-field correspondence):
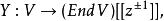 頂點代數
頂點代數給 V中每一向量配上一支以運算元為值之形式分布(formal distribution),稱作“ 頂點運算元”;其物理意義為在原點插入一運算元。T則是無窮小位移之一生成元。 “四頂點函式”公理統一了(誤差不過奇異值之)結合律與交換律。 位移公理涵蘊Ta = a 1, 故Y的值決定了T的值。
分階頂點代數
一 Z- 分階頂點代數為一頂點代數V的分階:
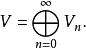 頂點代數
頂點代數使每a∈ V與b∈ V, 符合ab∈ V。
設有一 Z-分階頂點代數。 其一 Virasoro 元 為V中一元 ω , 使頂點運算元
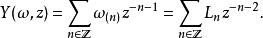 頂點代數
頂點代數符合以下條件:V中每一元a符合:
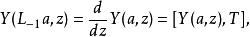 頂點代數
頂點代數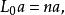 頂點代數
頂點代數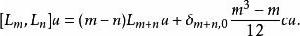 頂點代數
頂點代數其中 為一常值,稱“中心荷”(central charge), 或“ 之秩”。 此亦使 成為Virasoro 代數的一表示。
