定義
 泊松代數
泊松代數一個泊松代數是域K上一個向量空間裝備著兩個雙線性乘積, 與 { , },滿足如下性質:
 泊松代數
泊松代數(1)乘積 構成一個結合K-代數;
(2)乘積 { , },叫做泊松括弧,構成李代數,從而反對稱並滿足雅可比恆等式。
 泊松代數
泊松代數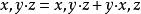 泊松代數
泊松代數(3)泊松括弧是結合乘積 的導子,即對此代數中任何三個元素x,y與z,都有 。
最後一個性質通常保證了這個代數有其他給出表述,可見下面例子中所指出。
例子
泊松代數出現於多種不同場合。
辛流形
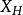 泊松代數
泊松代數辛流形上實值光滑函式組成一個泊松代數。辛流形上每個實值函式H在此流形上產生一個向量場 ,即哈密頓向量場。然後給定此辛流形上任何光滑函式 F與 G,它們的泊松括弧 {,} 定義為
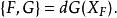 泊松代數
泊松代數這個定義是一致的是因為此泊松括弧是一個導子。等價地,可以將 {,} 定義為
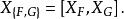 泊松代數
泊松代數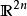 泊松代數
泊松代數這裡 [,] 是李導數。當辛流形是帶著標準辛結構的 ,則泊松括弧取如下熟知的形式
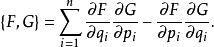 泊松代數
泊松代數可對泊松流形進行類似的考慮,它允許辛雙向量在流形的某些位置消沒。
結合代數
如果A是一個結合代數,則交換子 [x,y]≡xy−yx使它成為一個泊松代數。
頂點運算元代數
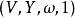 泊松代數
泊松代數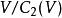 泊松代數
泊松代數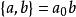 泊松代數
泊松代數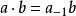 泊松代數
泊松代數對一個頂點運算元代數,空間 是一個泊松代數,其中 而 。對某些定點運算元代數,這個泊松代數是有限維的。
相關條目
•泊松超代數(Poisson superalgebra)
•格爾斯滕哈伯代數
•Moyal bracket
