離散的不等式
定義
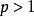赫爾德不等式
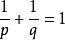赫爾德不等式
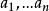赫爾德不等式
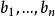赫爾德不等式設 ， 。令 和 是非負實數。 那么
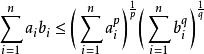赫爾德不等式成立條件
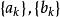赫爾德不等式
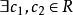赫爾德不等式
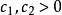赫爾德不等式
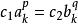赫爾德不等式
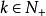赫爾德不等式僅當{ 中至少有一個為零數列或者 ，且 ,使得 ,
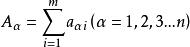赫爾德不等式
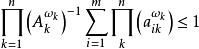赫爾德不等式證明：記,則式子
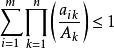赫爾德不等式即
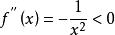赫爾德不等式因為f(x)=lnx(x>0)是向上凸函式（因為),由加權Jensen不等式，可得
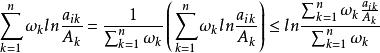赫爾德不等式
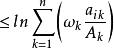赫爾德不等式
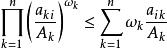赫爾德不等式所以
把上式對i到m求和 得：
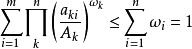赫爾德不等式從而命題得證。
連續的不等式
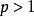赫爾德不等式 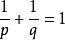赫爾德不等式
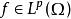赫爾德不等式
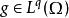赫爾德不等式假設 ， 。如果 ， ，那么
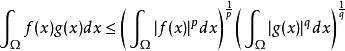赫爾德不等式離散形式
(有限和和無窮和)
內容
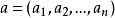赫爾德不等式
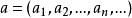赫爾德不等式設 或 為實數或複數列， a叫做多重指標，令
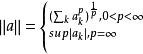赫爾德不等式滿足條件的 p,q稱為共軛指數，q=1是規定p=∞,
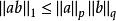赫爾德不等式若1≤p≤∞，則
若0<p<1,則不等號反向。
成立條件
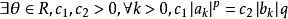赫爾德不等式
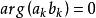赫爾德不等式1<p<∞時， ,且 成立
積分形式
內容
設p、q為共軛指數，令
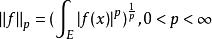赫爾德不等式
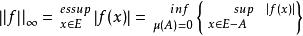赫爾德不等式
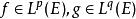赫爾德不等式若
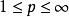赫爾德不等式
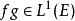赫爾德不等式
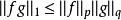赫爾德不等式當 時， ,且
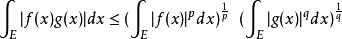赫爾德不等式
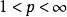赫爾德不等式即 , …………………… ①
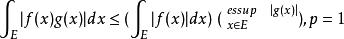赫爾德不等式………… …………②
若 0<p<1,則不等號方向改變
成立條件
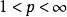赫爾德不等式
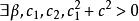赫爾德不等式
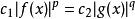赫爾德不等式
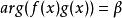赫爾德不等式時，僅當 ,使得 和 在E上幾乎處處成立時①式成立
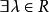赫爾德不等式
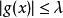赫爾德不等式
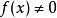赫爾德不等式
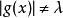赫爾德不等式p=1時，僅當 ，使得 a.e.(almost everywhere)於E，且 時， ②式成立
證明
如果|| f||= 0，那么 f在 μ-幾乎處處為零，且乘積 fg在 μ-幾乎處處為零，因此赫爾德不等式的左端為零。如果|| g||=0也是這樣。因此，我們可以假設|| f||>0且|| g||>0。
如果|| f||= ∞或|| g||=∞，那么不等式的右端為無窮大。因此，我們可以假設|| f||和|| g||位於(0,∞)內。
如果 p= ∞且 q= 1，那么幾乎處處有| fg| ≤ || f|||g|，不等式就可以從勒貝格積分的單調性推出。對於 p=1和 q=∞，情況也類似。因此，我們還可以假設 p, q∈ (1,∞)。
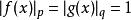赫爾德不等式分別用 f和 g除|| f|||| g||，我們可以假設：
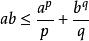赫爾德不等式我們現在使用楊氏不等式：
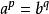赫爾德不等式對於所有非負的 a和 b，若且唯若時 等式成立。
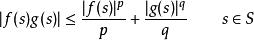赫爾德不等式因此：
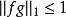赫爾德不等式兩邊積分，得：.
這便證明了赫爾德不等式。
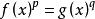赫爾德不等式
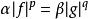赫爾德不等式在 p∈ (1,∞)和|| f||= || g||= 1的假設下，等式成立若且唯若幾乎處處有 。更一般地，如果|| f||和|| g||位於(0,∞)內，那么赫爾德不等式變為等式，若且唯若存在 α, β>0（即 α= || g||且 β= || f||），使得： μ-幾乎處處(*)
|| f||= 0的情況對應於(*)中的 β=0。|| g||=的情況對應於(*)中的 α=0。
