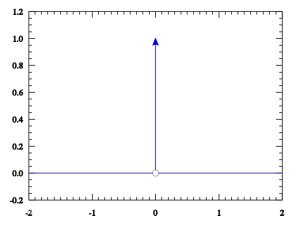
定義
物理學中常常要研究一個物理量在空間或時間中分布的密度,例如質量密度、電荷密度、每單位時間傳遞的動量(即力)等等,但是物理學中又常用到質點、點電荷、瞬時力等抽象模型,他們不是連續分布於空間或時間中,而是集中在空間中的某一點或者時間中的某一瞬時,那么它們的密度應該如何表示呢?
一種定義
為了在數學上理想地表示出這種密度分布,引入了δ函式的概念。在概念上,它是這么一個“函式”:在除了零以外的點函式值都等於零,而其在整個定義域上的積分等於1。用數學表示為:
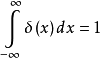 公式
公式 上述表達式不規定δ函式在0點的取值,是因為這個值無法嚴謹地表述出來,不能籠統的定義為正無窮,並且函式取值的“大小”是由第二個積分式決定的,因此只需限定取值為零的區域即可。如果函式不在0點取非零值,而在其他地方,可定義
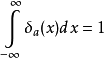 公式
公式另一種定義
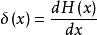 公式
公式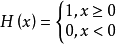 公式
公式理解
廣義函式
嚴格來說δ函式不能算是一個函式,因為滿足以上條件的函式是不存在的。數學上,人們為這類函式引入了廣義函式的概念,在廣義函式的理論中,δ函式的確切意義應該是在積分意義下來理解。在實際套用中,δ函式總是伴隨著積分一起出現。δ分布在偏微分方程、數學物理方法、傅立葉分析和機率論里都有很重要的套用。
近似形式
一些函式可以認為是狄拉克δ函式的近似,但是要注意,這些函式都是通過極限構造的,因此嚴格上都不是狄拉克δ函式本身,不過在一些數學計算中可以作為狄拉克δ函式進行計算。
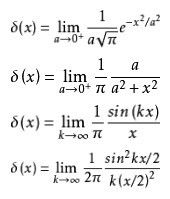 函式公式
函式公式性質
狄拉克δ函式有以下性質,在理解這些性質的時候,應該認為等式兩邊分別作為被積函式的因子時得到的結果相等。對稱性
δ(X)偶函式,其導數是奇函式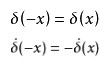 函式公式
函式公式放縮
放縮(或相似性)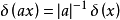 函式公式
函式公式挑選性
 函式公式
函式公式