狄利克雷級數
正文
又稱指數級數,即形如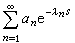 (1)
(1)
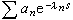 ,式中 αn是復常數;
,式中 αn是復常數;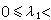
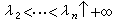 ;s=σ+it;σ及t是實變數。若(1)收斂,則記其和為ƒ(s)。當λn=n時,級數(1)是e-s的冪級數,其性質可由冪級數的性質推出,由此啟示人們研究一般指數級數的性質。當λn=lnn時,級數(1)成為
;s=σ+it;σ及t是實變數。若(1)收斂,則記其和為ƒ(s)。當λn=n時,級數(1)是e-s的冪級數,其性質可由冪級數的性質推出,由此啟示人們研究一般指數級數的性質。當λn=lnn時,級數(1)成為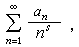 這是P.G.L.狄利克雷在解析數論中引用的重要級數;在αn=1的最簡單的情形,它稱為黎曼 ζ函式。此外,把狄利克雷級數推廣到積分的情形就是拉普拉斯變換,因此兩者有很多類似之處。
這是P.G.L.狄利克雷在解析數論中引用的重要級數;在αn=1的最簡單的情形,它稱為黎曼 ζ函式。此外,把狄利克雷級數推廣到積分的情形就是拉普拉斯變換,因此兩者有很多類似之處。 收斂性 對一般指數級數有阿貝爾型的定理:設級數(1)在一點s0收斂,則它在任何角域│arg(s-s0)│≤у(<π/2)中一致收斂。這樣,如級數(1)在一點
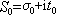 收斂(絕對收斂),則它在任何點s=σ+it(σ>σ0)收斂(絕對收斂)。於是級數(1)屬於下列三種情況之一:①存在著有限數 σ0(σα),級數在半平面σ>σ0(σ>σα)內收斂(絕對收斂),在半平面σ<σ0(σ<σα)內發散(不絕對收斂)。這時σ0(σα)稱為級數 (1)的收斂橫坐標(絕對收斂橫坐標),σ>σ0(σ>σα)稱為收斂半平面(絕對收斂半平面),σ=σ0(σ=σα)稱為收斂軸(絕對收斂軸)。②對任何 s=σ+it,級數發散(不絕對收斂),這時稱級數(1)的收斂(或絕對收斂)橫坐標為+
收斂(絕對收斂),則它在任何點s=σ+it(σ>σ0)收斂(絕對收斂)。於是級數(1)屬於下列三種情況之一:①存在著有限數 σ0(σα),級數在半平面σ>σ0(σ>σα)內收斂(絕對收斂),在半平面σ<σ0(σ<σα)內發散(不絕對收斂)。這時σ0(σα)稱為級數 (1)的收斂橫坐標(絕對收斂橫坐標),σ>σ0(σ>σα)稱為收斂半平面(絕對收斂半平面),σ=σ0(σ=σα)稱為收斂軸(絕對收斂軸)。②對任何 s=σ+it,級數發散(不絕對收斂),這時稱級數(1)的收斂(或絕對收斂)橫坐標為+ 。③對任何s=σ+it,級數收斂(絕對收斂),這時稱級數(1)的收斂(絕對收斂)橫坐標為-
。③對任何s=σ+it,級數收斂(絕對收斂),這時稱級數(1)的收斂(絕對收斂)橫坐標為- 。
。 對級數 (1)還可引進一致收斂橫坐標的概念。級數(1)的一致收斂橫坐標是
 。
。
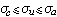 。當λn=n時,
。當λn=n時,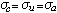 ,但這在一般情形下不成立,例如對於
,但這在一般情形下不成立,例如對於 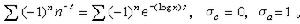
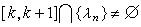 ,設
,設 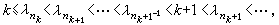
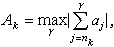

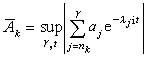
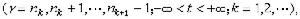
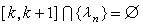 ,則令
,則令 。於是
。於是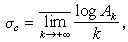

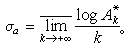
關於收斂橫坐標還有一個簡單的不等式:
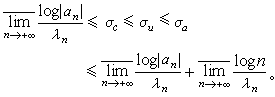
係數的表示和估計 如σα<+
 ,那么對於σ1>σα,
,那么對於σ1>σα, 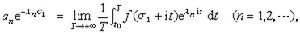 式中t0是任一實數。由此可得柯西不等式的推廣:
式中t0是任一實數。由此可得柯西不等式的推廣: 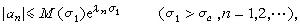 (2)
(2)
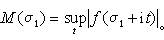
關於冪級數的奇異點、增長性、值的分布以及求和法等方面許多結果,都可推廣到指數級數。
參考書目
S. Mandelbrojt,Séries de Dirichlet, Gauthier-Villars,Paris, 1969.
S.Mandelbrojt,Séries Adhérentes etc.,Gauthier-Villars,Paris, 1952.