基本方法
方法
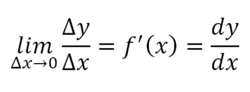 求導基本格式
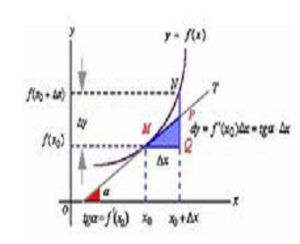
求導基本格式⑴求函式y=f(x)在x處導數的步驟:
① 求函式的增量Δy=f(x+Δx)-f(x)
② 求平均變化率
③ 取極限,得導數。
⑵基本初等函式的導數公式:
1.C'=0(C為常數);
2.(X)'=nX (n∈Q);
3.(sinX)'=cosX;
4.(cosX)'=-sinX;
5.(a)'=aIna (ln為自然對數)
特別地,(e)'=e
6.(logX)'=(1/X)loge=1/(Xlna) (a>0,且a≠1)
特別地,(ln x)'=1/x
7.(tanX)'=1/(cosX)=(secX)
8.(cotX)'=-1/(sinX)=-(cscX)
9.(secX)'=tanX secX
10.(cscX)'=-cotX cscX
⑶導數的四則運算法則:
①(u±v)'=u'±v'
②(uv)'=u'v+uv'
③(u/v)'=(u'v-uv')/ v
④複合函式的導數
[u(v)]'=[u'(v)]*v',(u(v)為複合函式f[g(x)])
複合函式對自變數的導數,等於已知函式對中間變數的導數,乘以中間變數對自變數的導數--稱為鏈式法則。
導數是微積分的基礎,同時也是微積分計算的一個重要的支柱。
重要極限
當 x 趨於0時 sin x=tan x=x
當 x 趨於0時 (1+x)=e
上式等價於 當 x 趨於正無窮時,(1+1/x)=e
部分證明
(a)'=aIna
b為一個趨於0的量
(f(x+b)-f(x)) / b
=(a-a)/b
=a(a-1)/b
令c=a-1,則c是一個趨於0的量
故b=loga(c+1)
所以上式變為a*c/loga(c+1)
=a*c/(c*loga((c+1)))
=a*c/(c*logae)
=a/logae
=alna
(logaX)'=(1/X)logae=1/(Xlna) (a>0,且a≠1)
b為一個趨於0的量
(f(x+b)-f(x)) / b
=loga(1+b/x)/b
=(b/x)*(loga((1+b/x)))/b
=logae/x
=1/(x*ln a)
註明
不是所有的函式都可以求導!可導的函式一定連續,但連續的函式不一定可導!比如y=|x|在y=0處不可導。
表示
用()'表示
套用實例
程式套用
diff(函式),求函式的一階導數;
diff(函式,n),求函式的n階導數(n是具體整數);
diff(函式,變數名),求對變數的偏導數;
diff(函式,變數名,n),求對的n階偏導數;
matlab求雅可比矩陣命令jacobian,調用格式:
jacobian([函式;函式;函式],[])給出矩陣:
實例
下面給出的是求函式x^2的導數的例子.
輸入:syms x;
diff(x^2);
可以得到結果:
ans =
2*x
分析:
如果一個極限過程你發現分母為零,那就看分子是不是零。
如果分子也是零,或者嘗試一下再化簡,能把分子分母共同的無窮小量給約掉,
或用洛必達法則;
如果分子不是零,就意味著這個極限是無窮,也即發散的。