阿貝爾範疇間的正合函子
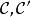 正合函子
正合函子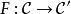 正合函子
正合函子設 為阿貝爾範疇, 為加法函子。若對每個正合序列
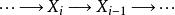 正合函子
正合函子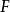 正合函子
正合函子取 後得到的序列
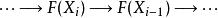 正合函子
正合函子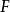 正合函子
正合函子仍為正合序列,則稱 為 正合函子。
由於正合序列總能拆解為短正合序列,在定義中僅須考慮短正合序列即可。
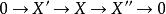 正合函子
正合函子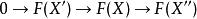 正合函子
正合函子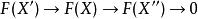 正合函子
正合函子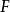 正合函子
正合函子此外,若對每個短正合序列 ,其像截去尾端零對象後 為正合序列,則稱 左正合函子;類似地,若 為正合序列,則稱 是 右正合函子。正合性等價於左正合性+右正合性。
一般範疇中的正合函子
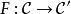 正合函子
正合函子考慮一個函子 。
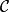 正合函子
正合函子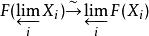 正合函子
正合函子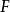 正合函子
正合函子若 里存在任意的有限射影極限,且與有限射影極限交換(即: ),則稱 為 左正合。
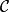 正合函子
正合函子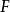 正合函子
正合函子 正合函子
正合函子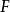 正合函子
正合函子若 里存在任意的有限歸納極限,且 與有限歸納極限交換(即: ),則稱 為 右正合。
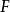 正合函子
正合函子若上述條件同時被滿足,則稱 為 正合。
在阿貝爾範疇中,由於任意有限射影(或歸納)極限可以由核(或上核)與有限積(或上積)生成,此時的定義遂回歸到正合序列的定義。
例子
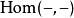 正合函子
正合函子根據極限的泛性質, 函子無論對哪個變數都是左正合的,這是左正合函子的基本例子。
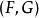 正合函子
正合函子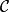 正合函子
正合函子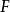 正合函子
正合函子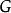 正合函子
正合函子設 是一對伴隨函子。若 存在任意有限歸納極限,則 右正合;若存在任意有限射影極限, 左正合。此法可建立許多函子的正合性。
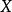 正合函子
正合函子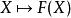 正合函子
正合函子設 為拓撲空間,阿貝爾群數學範疇上的整體截面函子 是左正合函子。
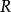 正合函子
正合函子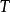 正合函子
正合函子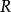 正合函子
正合函子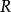 正合函子
正合函子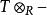 正合函子
正合函子設 為環, 為右 -模,則左 -模範疇上的張量積函子 是右正合函子。
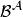 正合函子
正合函子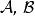 正合函子
正合函子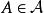 正合函子
正合函子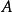 正合函子
正合函子設 為兩個阿貝爾範疇,考慮函子範疇,固定一對象 ,對 的“求值”是正合函子。
