基本介紹
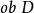 全子範疇
全子範疇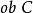 全子範疇
全子範疇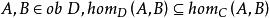 全子範疇
全子範疇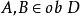 全子範疇
全子範疇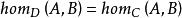 全子範疇
全子範疇範疇D稱為C的 子範疇(sub category),如果 是 的子類,且 ,而且D中的態射的合成和C是一樣的。例如,Poset是Set的子範疇。又如果 ,有 ,則稱D是C的 全 子範疇(full subcategory)。例如,Grp是Mon的全子範疇。
相關概念
模範疇對偶性
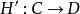 全子範疇
全子範疇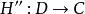 全子範疇
全子範疇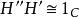 全子範疇
全子範疇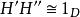 全子範疇
全子範疇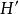 全子範疇
全子範疇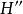 全子範疇
全子範疇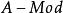 全子範疇
全子範疇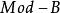 全子範疇
全子範疇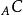 全子範疇
全子範疇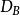 全子範疇
全子範疇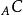 全子範疇
全子範疇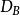 全子範疇
全子範疇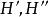 全子範疇
全子範疇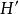 全子範疇
全子範疇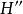 全子範疇
全子範疇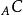 全子範疇
全子範疇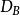 全子範疇
全子範疇模範疇對偶性(duality in categories of modules)是模範疇等價的對偶概念。設C和D是兩個範疇, 和 是兩個逆變函子,若有自然等價 和 ,則稱 與 是對偶函子,而稱C與D是對偶範疇。模論中考慮較多的問題是:在模範疇 和 中是否有全子範疇 和 ,以及 和 之間的加性逆變函子 ,使得 與 是對偶函子, 和 是對偶範疇,此性質就稱為模範疇的對偶性。
模範疇等價
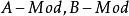 全子範疇
全子範疇模範疇等價(equivalence of categories of modules)是對模範疇的一種刻畫,存在等價函子的模範疇稱為等價的模範疇。設 是模範疇,若存在加性共變函子
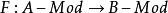 全子範疇
全子範疇和
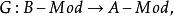 全子範疇
全子範疇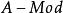 全子範疇
全子範疇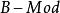 全子範疇
全子範疇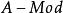 全子範疇
全子範疇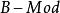 全子範疇
全子範疇使得GF自然同構於 的恆等函子,FG自然同構於 的恆等函子,則稱函子F與G等價,且稱模範疇 與 是等價的,記為
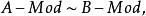 全子範疇
全子範疇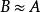 全子範疇
全子範疇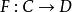 全子範疇
全子範疇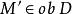 全子範疇
全子範疇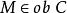 全子範疇
全子範疇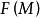 全子範疇
全子範疇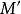 全子範疇
全子範疇此時,也稱環A與B是森田紀一相似的,記為 。兩個模範疇C,D等價的充分必要條件是,存在全忠實函子 ,並且對任意 ,總有 ,使得 同構於 。模範疇的等價理論是模論的一個重要組成部分,森田紀一(Morita Kiiti)於1958年討論了兩個模範疇的等價和對偶,得到了一系列深刻而又漂亮的結果,森田紀一的工作是經典的阿廷-韋德伯恩定理在模上的推廣,現在他的工作已發展成所謂的森田紀一理論。
森田紀一對偶定理
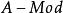 全子範疇
全子範疇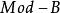 全子範疇
全子範疇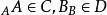 全子範疇
全子範疇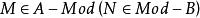 全子範疇
全子範疇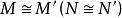 全子範疇
全子範疇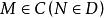 全子範疇
全子範疇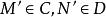 全子範疇
全子範疇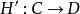 全子範疇
全子範疇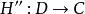 全子範疇
全子範疇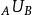 全子範疇
全子範疇森田紀一對偶定理(Morita theorem on duality)是模範疇對偶性的重要定理。設C和D是 和 的全子範疇,且 ,又對任意 ,若 ,則必有 ,這裡 。若 和 是對偶函子,則一定存在雙模 ,使得:
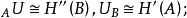 全子範疇
全子範疇1.
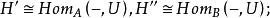 全子範疇
全子範疇2.
3. C和D中每個模都是U自反模。
在一個模範疇中,不可能每一個模都是U自反模,所以模範疇的對偶只能在全子範疇之間存在。
塞爾子範疇
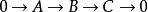 全子範疇
全子範疇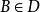 全子範疇
全子範疇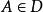 全子範疇
全子範疇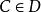 全子範疇
全子範疇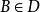 全子範疇
全子範疇塞爾子範疇(Serre subcategory)是阿貝爾範疇的一種子範疇,它在同調代數等學科中有重要套用,也是定義商範疇的基礎概念。設C為阿貝爾範疇,D為C的全子範疇且滿足:對C中任意的正合列 , 若且唯若 且 (即, 若且唯若B的子對象與商對象都是D的對象),此時稱D為C的塞爾子範疇,塞爾子範疇仍為阿貝爾範疇。

