求法
等差數列
對於一個數列{ a},如果任意相鄰兩項之差為一個常數,那么該數列為等差數列,且稱這一定值差為公差,記為 d ;從第一項 a到第n項 a的總和,記為S 。
那么 , 通項公式為
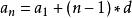 數列通項公式
數列通項公式,其求法很重要,利用了“疊加原理”的思想:
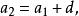 數列通項公式
數列通項公式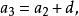 數列通項公式
數列通項公式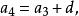 數列通項公式
數列通項公式 數列通項公式
數列通項公式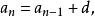 數列通項公式
數列通項公式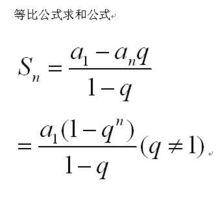 數列通項公式
數列通項公式將以上 n-1 個式子相加, 便會接連消去很多相關的項 ,最終等式左邊餘下a ,而右邊則餘下a和 n-1 個d,如此便得到上述通項公式。
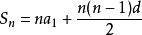 數列通項公式
數列通項公式此外, 數列前 n 項的和 ,其具體推導方式較簡單,可用以上類似的疊加的方法,也可以採取疊代的方法,在此,不再複述。
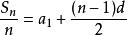 數列通項公式
數列通項公式值得說明的是, ,也即,前n項的和S 除以 n 後,便得到一個以a 為首項,以 d /2 為公差的新數列,利用這一特點可以使很多涉及S的數列問題迎刃而解。
等比數列
對於一個數列 {a},如果任意相鄰兩項之商(即二者的比)為一個常數,那么該數列為等比數列,且稱這一定值商為公比 q ;從第一項a 到第n項a 的總和,記為T 。
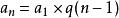 數列通項公式
數列通項公式那么, 通項公式為 (即a 乘以q 的 (n-1)次方,其推導為“連乘原理”的思想:
a=a * q,
a= a * q,
a= a * q,
````````
a=a * q,
將以上(n-1)項相乘,左右消去相應項後,左邊餘下a , 右邊餘下a和(n-1)個q的乘積,也即得到了所述通項公式。
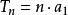 數列通項公式
數列通項公式此外, 當q=1時 該數列的前n項和
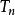 數列通項公式
數列通項公式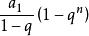 數列通項公式
數列通項公式當q≠1時 該數列前n 項的和 =
一階數列
概念
不妨將數列遞推公式中同時含有a 和a的情況稱為一階數列,顯然,等差數列的遞推式為
a=a + d , 而等比數列的遞推式為 a=a * q ; 這二者可看作是一階數列的特例。故可定義一階遞歸數列形式為: a= A *a + B ········☉ , 其中A和B 為常係數。那么,等差數列就是A=1 的特例,而等比數列就是B=0 的特例。
思路
基本思路與方法: 複合變形為基本數列(等差與等比)模型 ; 疊加消元 ;連乘消元
思路一: 原式複合 ( 等比形式)
可令a - ζ = A * (a - ζ )········① 是原式☉變形後的形式,即再採用待定係數的方式求出 ζ 的值, 整理①式 後得a = A*a + ζ - A*ζ , 這個式子與原式對比可得,
ζ - A*ζ = B
即解出 ζ = B / (1-A)
回代後,令 b=a - ζ ,那么①式就化為b =A*b , 即化為了一個以(a- ζ )為首項,以A為公比的等比數列,可求出b的通項公式,進而求出 {a} 的通項公式。
思路二: 消元複合(消去B)
由 a = A *a + B ········☉ 有
a = A* a +B ··········◎
☉式減去◎式可得 a - a = A *( a - a)······③
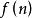 數列通項公式
數列通項公式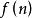 數列通項公式
數列通項公式令b= a - a 後, ③式變為b = A*b 等比數列,可求出b 的通項公式,接下來得到 a - a = (其中 為關於n的函式)的式子, 進而使用疊加方法可求出 a
二階數列
概念
類比一階遞歸數列概念,不妨定義同時含有a 、a、a的遞推式為二階數列,而對與此類數列求其通項公式較一階明顯難度大了。為方便變形,可以先如此詮釋二階數列的簡單形式:
a = A * a +B * a , ( 同樣,A,B常係數)
思路
基本思路類似於一階,只不過,在複合時要注意觀察待定係數和相應的項
原式複合: 令 原式變形後為這種形式 a - ψ * a= ω (a - ψ * a)
將該式與原式對比 ,可得
ψ + ω = A 且 -(ψ*ω)= B
通過解這兩式可得出 ψ與ω的值,
令b= a - ψ*a, 原式就變為b = ω *b 等比數列,可求出b 通項公式b= f (n) ,
即得到 a - ψ*a = f (n) (其中f(n) 為關於n的函式), 而這個式子恰複合了一階數列的定義,即只含有a和a 兩個數列變項,從而實現了“降階”,化“二階”為“一階”,進而求解。
常見類型
累加法
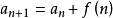 數列通項公式
數列通項公式遞推公式為 ,且f(n)可以求和
例:數列{a},滿足a=1/2,a= a+ 1/(4n -1),求{a}通項公式
解:a= a+ 1/(4n -1)=an+[1/(2n-1)-1/(2n+1)]/2
∴a = a+(1-1/3+1/3-1/5+……+1/(2n-3)-1/(2n-1))
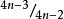 數列通項公式
數列通項公式∴a= 1/2+1/2 (1-1/(2n-1) )=
累乘法
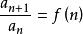 數列通項公式
數列通項公式遞推公式為 且f(n)可求積
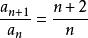 數列通項公式
數列通項公式例:數列{a}滿足 ,且a=4,求a
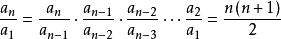 數列通項公式
數列通項公式解:
a= 2n(n+1)
構造法
將非等差數列、等比數列,轉換成相關的等差等比數列
適當的進行運算變形
例:{a} 中,a=3且 a= a, 求a
解:ln a= ln a= 2 ln a
∴{ln a}是等比數列,其中公比q = 2,首項為ln3
∴ln a = (2) ln3
故
倒數變換法(適用於a= A*a/ (B*a+ C),其中,A、B、C∈R)
例:{a}中,a=1,a= a / ( 2a+ 1 )
解:1 / a= ( 2a+1 ) / a= 1/a +2
∴{1/a}是等差數列,首項是1,公差是2
∴a= 1 / (2n-1)
待定係數法
A.遞推式為a= p*a+ q(p,q為常數),可以構造遞推數列{a+ x}為 以p為公比的等比數列,
即a+ x=p*(a+x),其中 x = q / (p-1) (或者可以把設定的式子拆開,等於原式子)
例:{a}中a=1,a= 3a+4,求a
解:a+ 2 = 3(a+2)
∴{a+2}是等比數列 首項是3,公比是3
∴a= 3- 2
B.遞推公式為a = p*a+ q(p,q是常數)
常規變形,將兩邊同時除以q
得到a / q= (p / q)*( a/q)+1/q
再令b= a/ q,
可以得到b= k*b+ m(其中k=p/q , m=1/q)
之後就用上面A中提到的方法來解決
C.遞推公式為a= p*a+q*a,(p,q是常數)
可以令a=x , a= x , a= 1
解出x和x,可以得到兩個式子
a - xa= x(a- xa)
a- xa=x(a- xa)
然後,兩式子相減,左邊可以得出來 (k為係數)
右邊就用等比數列的方法得出來
例:{a}中,a=1, a=2, a= (2/3)a=(1/3) a
解:x= 2x/3 = 1/3
x=1,x=-1/3
可以得到方程組
a- a= - (1/3)* (a- a)
a+(1/3)* a= a+ (1/3)*a
解得a= 7/4 - 3/4×(-1/3)^(n-1)
D.遞推式a= p* a+ a+b(a,b,p是常數)
可以變形為a+ x+y = p*(a+ x+ y)
然後和原式子比較,可以得出x,y,
即可以得到{a+x+y}是個 以p為公比的等比數列
例:{a}中,a=4, a=3a+ 2n-1 (n≥2)
解:原式= a+ n+1= 3 [a+ (n-1)+1]
∴{a+n+1}為等比數列,q=3,首項是6
∴a= 2×3- n - 1
特徵根法
遞推式為a= (A*a+B) / (C*a+D) (A,B,C,D是常數)
令a= a= x,原式則為x = (Ax+B) / (Cx+D)
(1)若解得相同的實數根x,則可以構造數列{1/(a-x)}為等差數列
例:{a}滿足a= 2,a= (2a-1)/(4a+6),求a
解:x = (2x-1) / (4x+6)
解得x= - 1/2
1/(a+1/2)=1/[(2a-1)/(4a+6) +1/2]=1/[a+ 1/2] +1
∴{1/(a+ 1/2)}是等差數列,d=1,首項是2/5
∴an=5/(5n-3) -1/2
(2)若解得兩個相異實根x,x,則構造{(a- x)/(a- x)}為等比數列(x,x的位置沒有順序,可以調換)
例:{a}滿足a= 2,a= (a+2)/(2a+1)
解:由題可得(a-1)/(a+1)=-1/3 [a- 1]/[a+ 1]
則{(a-1)/(a+1)}是等比數列,q=-1/3,首項是1/3
∴a = [1 + (-1) (1/3)] / [1 - (-1) (1/3)]
(3)如果沒有實數根,那么這個數列可能是周期數列
例:{a}中,a= 2,滿足a= a/ a(n≥2)
解:a= 2 , a= 1/2 , a= -1 , a= 2 , a= 1/2 ……
所以a= 2(n MOD 3 = 1),1/2(n MOD3 = 1),-1(n MOD 3 = 0)
(準確的應該是有大括弧像分段函式那樣表示,但是這裡無法顯示)
1.適當的進行運算變形
例:{a} 中,a=3且 a= a, 求a
解:ln a= ln a= 2 ln a
∴{ln a}是等比數列,其中公比q = 2,首項為ln3
∴ln a = (2) ln3
故
2.倒數變換法(適用於a= A*a/ (B*a+ C),其中,A、B、C∈R)
例:{a}中,a=1,a= a / ( 2a+ 1 )
解:1 / a= ( 2a+1 ) / a= 1/a +2
∴{1/a}是等差數列,首項是1,公差是2
∴a= 1 / (2n-1)
3.待定係數法
A.遞推式為a= p*a+ q(p,q為常數),可以構造遞推數列{a+ x}為 以p為公比的等比數列,
即a+ x=p*(a+x),其中 x = q / (p-1) (或者可以把設定的式子拆開,等於原式子)
例:{a}中a=1,a= 3a+4,求a
解:a+ 2 = 3(a+2)
∴{a+2}是等比數列 首項是3,公比是3
∴a= 3- 2
B.遞推公式為a = p*a+ q(p,q是常數)
常規變形,將兩邊同時除以q
得到a / q= (p / q)*( a/q)+1/q
再令b= a/ q,
可以得到b= k*b+ m(其中k=p/q , m=1/q)
之後就用上面A中提到的方法來解決
C.遞推公式為a= p*a+q*a,(p,q是常數)
可以令a=x , a= x , a= 1
解出x和x,可以得到兩個式子
a - xa= x(a- xa)
a- xa=x(a- xa)
然後,兩式子相減,左邊可以得出來 (k為係數)
右邊就用等比數列的方法得出來
例:{a}中,a=1, a=2, a= (2/3)a=(1/3) a
解:x= 2x/3 = 1/3
x=1,x=-1/3
可以得到方程組
a- a= - (1/3)* (a- a)
a+(1/3)* a= a+ (1/3)*a
解得a= 7/4 - 3/4×(-1/3)^(n-1)
D.遞推式a= p* a+ a+b(a,b,p是常數)
可以變形為a+ x+y = p*(a+ x+ y)
然後和原式子比較,可以得出x,y,
即可以得到{a+x+y}是個 以p為公比的等比數列
例:{a}中,a=4, a=3a+ 2n-1 (n≥2)
解:原式= a+ n+1= 3 [a+ (n-1)+1]
∴{a+n+1}為等比數列,q=3,首項是6
∴a= 2×3- n - 1
4.特徵根法
遞推式為a= (A*a+B) / (C*a+D) (A,B,C,D是常數)
令a= a= x,原式則為x = (Ax+B) / (Cx+D)
(1)若解得相同的實數根x,則可以構造數列{1/(a-x)}為等差數列
例:{a}滿足a= 2,a= (2a-1)/(4a+6),求a
解:x = (2x-1) / (4x+6)
解得x= - 1/2
1/(a+1/2)=1/[(2a-1)/(4a+6) +1/2]=1/[a+ 1/2] +1
∴{1/(a+ 1/2)}是等差數列,d=1,首項是2/5
∴an=5/(5n-3) -1/2
(2)若解得兩個相異實根x,x,則構造{(a- x)/(a- x)}為等比數列(x,x的位置沒有順序,可以調換)
例:{a}滿足a= 2,a= (a+2)/(2a+1)
解:由題可得(a-1)/(a+1)=-1/3 [a- 1]/[a+ 1]
則{(a-1)/(a+1)}是等比數列,q=-1/3,首項是1/3
∴a = [1 + (-1) (1/3)] / [1 - (-1) (1/3)]
(3)如果沒有實數根,那么這個數列可能是周期數列
例:{a}中,a= 2,滿足a= a/ a(n≥2)
解:a= 2 , a= 1/2 , a= -1 , a= 2 , a= 1/2 ……
所以a= 2(n MOD 3 = 1),1/2(n MOD3 = 1),-1(n MOD 3 = 0)
(準確的應該是有大括弧像分段函式那樣表示,但是這裡無法顯示)
 數列通項公式
數列通項公式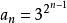 數列通項公式
數列通項公式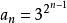 數列通項公式
數列通項公式連加相減
例:{a}滿足a₁+ 2a₂+ 3a₃+……+ na= n(n+1)(n+2)
解:令b= a₁+ 2a₂+ 3a₃+……+ na= n(n+1)(n+2)
na= b- b= n(n+1)(n+2)-(n-1)n(n+1)
∴a= 3(n+1)

