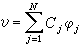慣量張量

簡介

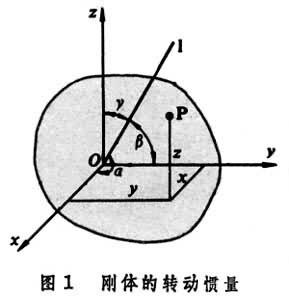
剛體對於一點的轉動慣性的量度。若Oxyz是固連在剛體上的一直角坐標系(圖1)，l軸是通過坐標原點O的任意軸,它和各坐標軸Ox、Oy、Oz的夾角分別為α、β、γ;設剛體中任一質點P的質量為mi，它的坐標為(xi,yi,zi)，則剛體對軸l的轉動慣量為式中為剛體對坐標軸Ox、Oy、Oz的轉動慣量。稱為慣性積。慣性積也依賴於剛體的質量、質量分布和各坐標軸的位置。但它的值可正可負，也可等於零。慣性積的量綱和轉動慣量相同，即等於ML2。剛體對過坐標原點O的任意軸l的轉動慣量I由六個量Ix、Iy、Iz、Ixy、Iyz、Izx及軸l對坐標軸Ox、Oy、Oz的方向餘弦決定。I是由剛體本身的質量、質量分布及軸l的方位來決定的，它是一個具有力學性質的量,它的值不因確定物體位置所選取的坐標系的不同而改變。對稱的慣量矩陣：是一個張量，稱為剛體關於原點O的慣量張量。

正文

剛體對於一點的轉動慣性的量度。若Oxyz是固連在剛體上的一直角坐標系(圖1)，l軸是通過坐標原點O的任意軸,它和各坐標軸Ox、Oy、Oz的夾角分別為α、β、γ;設剛體中任一質點P的質量為mi，它的坐標為(xi,yi,zi)，則剛體對軸l的轉動慣量為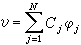

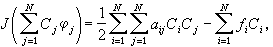
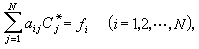
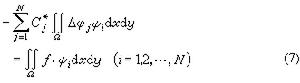式中為剛體對坐標軸Ox、Oy、Oz的轉動慣量。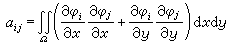

稱為慣性積。慣性積也依賴於剛體的質量、質量分布和各坐標軸的位置。但它的值可正可負，也可等於零。慣性積的量綱和轉動慣量相同，即等於ML2。
剛體對過坐標原點O 的任意軸l的轉動慣量I由六個量Ix、Iy、Iz、Ixy、Iyz、Izx及軸l對坐標軸Ox、Oy、Oz的方向餘弦決定。I是由剛體本身的質量、質量分布及軸l的方位來決定的，它是一個具有力學性質的量,它的值不因確定物體位置所選取的坐標系的不同而改變。對稱的慣量矩陣：

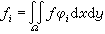
是一個張量，稱為剛體關於原點O 的慣量張量。

慣量張量

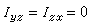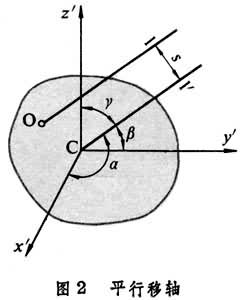
適當選擇坐標系Oxyz的方位,可使剛體的兩個慣性積同時為零，例如,，這時,和這兩個慣性積同時相關的z軸稱為剛體在O點處的一個慣量主軸。一般地說,對於剛體上的任意一點O有三個互相正交的慣量主軸。剛體對慣量主軸的轉動慣量稱為主轉動慣量。如果慣量主軸還通過剛體的質心，則這樣的主軸稱為中心慣量主軸，剛體對中心慣量主軸的轉動慣量稱為中心主轉動慣量。當剛體繞中心慣量主軸之一轉動時，在軸承上將不會由於轉動而引起附加的動反力（見剛體的定軸轉動）。
若Iс尣′、Iсу′、Iсz′為剛體對以中心慣量主軸為坐標軸Cx┡、Cy┡、Cz┡的轉動慣量(圖2),則通過O點的任意軸l的轉動慣量為

式中α、β、γ為平行於l軸且通過質心C的軸l┡和各坐標軸的夾角，m為剛體的質量，s為軸l和軸l┡之間的距離。可見，只要知道三個中心主轉動慣量，則可求出對任意軸l的轉動慣量。

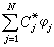
慣量張量

一般說來，確定慣量主軸的方向是困難的。但如果剛體的質量分布具有對稱軸，則該對稱軸便是慣量主軸，也是中心慣量主軸。若剛體的質量分布具有對稱面，垂直於這對稱面的任一直線是對於這直線和對稱面的交點的一個慣量主軸。如這交點和質心重合，則這軸是一個中心慣量主軸。均勻球體的任意三個互相正交的直徑是球體的三個中心慣量主軸。均勻橢球通過質心的三個幾何對稱軸是橢球的三個中心慣量主軸。

配圖

相關連線

大家都知道，剛體繞定軸轉動的角動量表達式為：
L=∑(r×Δmv)=∑Δmr×(ω×r)
此處我們為了顯得簡潔，去掉了每個腳標i。
假如這個剛體只繞z軸鏇轉，那么現在位置矢量r與角速度ω為：
r=(x,y,z)
ω=(0,0,ω)
現在，我們用矢量計算Lx、Ly和Lz，得到：
Lx=ω·∑(-xzΔm)
Ly=ω·∑(-yzΔm)
Lz=ω·∑(x²+y²)Δm
我們很熟悉Lz，它就是通常我們見到的Lz=Iω，但是，Lx=ω·∑(-xzΔm)和Ly=ω·∑(-yzΔm)是什麼？它們為什麼是這樣？
現在就讓我們來揭開這個秘密，因為雖然從數學上可以得到這兩項，卻不能理解它，將是一種缺憾——當然你可以不在乎，你可以只認為這兩項是其它坐標軸對這個坐標軸的貢獻，但是真正去了解一下“為什麼”將是有好處的。
我們只舉一個例子——x軸方向的多餘分量。
假設一塊剛體繞z軸逆時針正向轉動（右手法則！），那么對於x軸而言，根據同樣的法則，剛體上面的某一個小塊相對於x軸的速度將是與右手法則相反的（大拇指在x軸，看一看四指方向是否與小塊速度方向相反。請自己畫圖或想像）。
當小塊恰好在xoz平面上時，由於小塊繞z軸的角速度是ω，而離z軸的距離是x，所以小塊的線速度應該是v=xω。對於x軸而言，小塊離x軸距離為z，瞬時“繞”x軸的角動量就應該是z·Δmv。但是這與右手法則方向相反，所以應該加上一個負號，再對每個小塊求合：
Lx=∑-ωxz·Δm=ω·∑(-xzΔm)
我們考慮的是在xoz平面中的小塊，但不能總要求小塊在這個平面內，在求合的時候，其它很多小塊都不在這個平面內，但是這些物理量總會有一個投影在我們需要的平面中，所以上面的式子還是正確的。
對於自由的、繞不固定軸轉動的剛體，轉動慣量就應該寫成一個有9個元素的矩陣（張量）形式：
|∑m(y²+z²)-∑mxy-∑mxz|
I{ij}=|-∑myx∑m(x²+z²)-∑myz|
|-∑mzx-∑mzy∑m(x²+y²)|
而角動量就寫成這樣的張量表達形式： L{i}=I{ij}ω{j}