基礎知識
子圖的定義
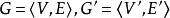 子圖
子圖 子圖
子圖 子圖
子圖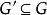 子圖
子圖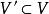 子圖
子圖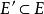 子圖
子圖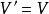 子圖
子圖設 為兩個圖(同為無向圖或同為有向圖),若 且 ,則稱G'是G的 子圖,G是G‘的 母圖,記作 ,又若 且 ,則G'稱是G的 真子圖,若 ,則稱G'是G的 生成子圖。
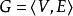 子圖
子圖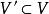 子圖
子圖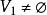 子圖
子圖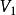 子圖
子圖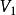 子圖
子圖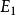 子圖
子圖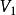 子圖
子圖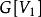 子圖
子圖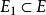 子圖
子圖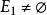 子圖
子圖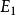 子圖
子圖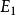 子圖
子圖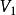 子圖
子圖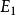 子圖
子圖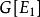 子圖
子圖設 為一圖, 且 ,稱以 為頂點集,以G中兩個端點都在 中的邊組成邊集 的圖為G的 導出子圖,記作 ,又設 且 ,稱以 為邊集,以 中邊關聯的頂點為頂點集 的圖為G的 導出的子圖,記作。
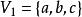 子圖
子圖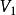 子圖
子圖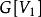 子圖
子圖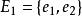 子圖
子圖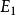 子圖
子圖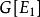 子圖
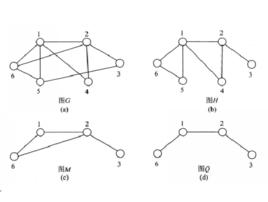
子圖在圖1中,設G如圖1(a)所示,取 ,則 的導出子圖 如圖1(b)所示,取 ,則 的導出子圖 如圖1(c)所示。
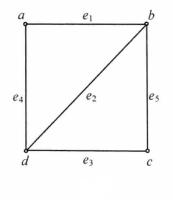 圖1(a)
圖1(a)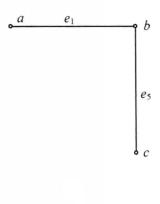 圖1(b)
圖1(b)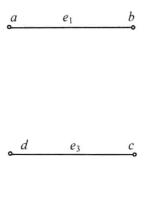 圖1(c)
圖1(c)補圖
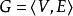 子圖
子圖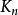 子圖
子圖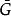 子圖
子圖設 為n階無向簡單圖,以V為頂點集,以所有使G成為完全圖的 的添加邊組成的集合為邊集的圖,稱為G的 補圖,記作。
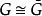 子圖
子圖若圖 ,則稱G是自補圖。
圖2中,(b)和(c)互為補圖,(a)是自補圖。
 圖2(a)
圖2(a)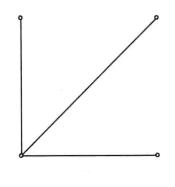 圖2(b)
圖2(b)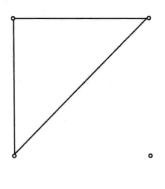 圖2(c)
圖2(c)相關定理
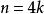 子圖
子圖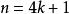 子圖
子圖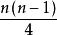 子圖
子圖若n階圖G是自補圖,則或,k為非負整數,且圖G有條邊。
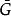 子圖
子圖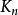 子圖
子圖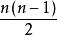 子圖
子圖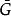 子圖
子圖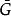 子圖
子圖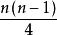 子圖
子圖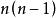 子圖
子圖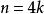 子圖
子圖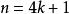 子圖
子圖證明:因為n階圖G是自補圖,所以G與同構。於是完全圖的條邊將各有一半為G與的邊,即G與均有條邊。而圖G的邊數是非負整數,故4一定能整除,而連續的兩個整數n-1與n總是一個為奇數,一個為偶數,故或(k為非負整數)。證畢。
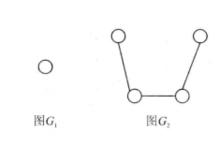 圖3(a)
圖3(a)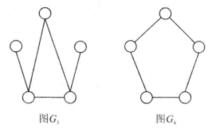 圖3(b)
圖3(b)圖的操作
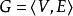 子圖
子圖設為無向圖。
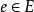 子圖
子圖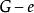 子圖
子圖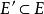 子圖
子圖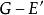 子圖
子圖(1)設,用表示從G中去掉邊e,稱為 刪除邊e。又設,用表示從G中刪除E'中的所有邊,稱為刪除E'。
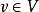 子圖
子圖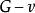 子圖
子圖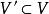 子圖
子圖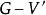 子圖
子圖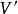 子圖
子圖(2)設,用表示從G中去掉v及所關聯的一切邊,稱為 刪除頂點v,又設,用表示從G中刪除中的所有邊,稱為刪除V'。
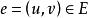 子圖
子圖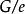 子圖
子圖(3)設邊,用表示從G中刪除e後,將e的兩個端點u,v用一個新的頂點w(或用u或用v充當w)代替,使w關聯e以外u,v關聯的所有邊,稱為邊e的 收縮。
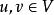 子圖
子圖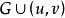 子圖
子圖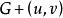 子圖
子圖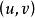 子圖
子圖(4)設(u,v可能相鄰,也可能不相鄰),用(或)表示在u,v之間加一條邊,稱為 加新邊。
在收縮邊和加新邊過程中可能產生環和平行邊。
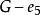 子圖
子圖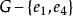 子圖
子圖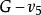 子圖
子圖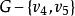 子圖
子圖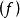 子圖
子圖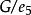 子圖
子圖在圖4中,設(a)圖為G,則(b)圖為,(c)圖為,(d)圖為,(e)圖為,而圖為。
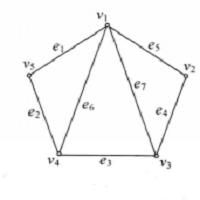 圖4(a)
圖4(a)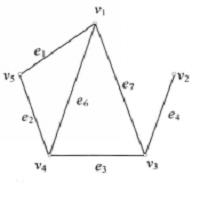 圖4(b)
圖4(b)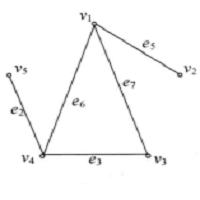 圖4(c)
圖4(c)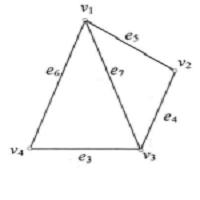 圖4(d)
圖4(d)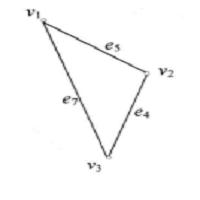 圖4(e)
圖4(e)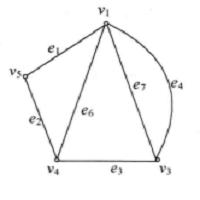 圖4(f)
圖4(f)