壓縮映射

設(X, ρ)為距離空間，T是X到X中的映射，如果存在數a(0

簡介

壓縮映射亦稱巴拿赫壓縮映射，是指在度量意義下壓縮的映射。

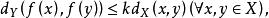壓縮映射

設(X,d)與(Y,d)是度量空間，f:X→Y是映射。若存在常數k∈[0,1)，使得 則稱f為壓縮映射，k稱為壓縮係數。

性質

壓縮映射必是連續映射，且為李普西茨連續。

當X為賦范線性空間，f:X→Y為壓縮映射時，映射I-f稱為X上的壓縮向量場。

映射

兩個非空集合A與B間存在著對應關係f，而且對於A中的每一個元素x，B中總有有唯一的一個元素y與它對應，就這種對應為從A到B的映射，記作f：A→B。其中，b稱為元素a在映射f下的象，記作：b=f(a)。a稱為b關於映射f的原象。集合A中所有元素的象的集合稱為映射f的值域，記作f(A)。

或者說，設A,B是兩個非空的集合，如果按某一個確定的對應關係f，使對於集合A中的任意一個元素x，在集合B中都有唯一的元素y與之對應，那么就稱對應f：A→B為從集合A到集合B的一個映射。