偏微分方程的基本解

偏微分方程的基本解

正文

偏微分方程的一種具有特定奇異性的解，由它可以構造出一般的解。例如對於二維和三維拉普拉斯方程的基本解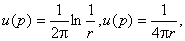 可用來構造出該方程的“通解”以及格林函式（見橢圓型偏微分方程）。對於三維的波動方程和熱傳導方程，它的基本解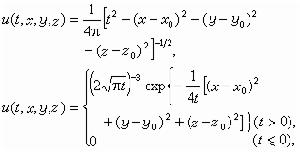

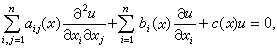
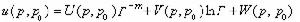也有類似的作用（見雙曲型偏微分方程、拋物型偏微分方程）。　 　J.（-S.）阿達馬對二階線性偏微分方程

在解析係數與非拋物（即det(αij)≠0）的條件，作出了以下形狀的基本解

,

式中U、V、W是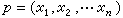,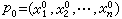的解析函式,Г是 p與p0在度量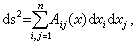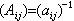下的測地距離的平方，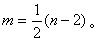
廣義函式是研究基本解的有力工具。線性偏微分運算元 l的基本解即適合下式的廣義函式E（p,p0）：l(E)=δ(p-p0),δ是狄喇克函式。當l為常係數運算元時,E(p,p0)=E(p-p0)。 若能作出E,則l(u)=ƒ將有解u=E*ƒ：l(E*ƒ)=l(E)*ƒ=δ*ƒ=ƒ。
對常係數偏微分運算元l,利用傅立葉變換可形式地作出基本解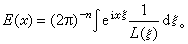這裡根本的困難是l(ξ)的零點將使該積分發散。20世紀50年代中期，L.赫爾曼德爾、B.馬爾格朗熱與L.埃倫普雷斯獨立克服了這個困難，證明了常係數線性偏微分運算元基本解的存在。這是偏微分方程論的重大進展。
對變係數線性偏微分運算元，則有必要將基本解概念推廣為擬基本解。在構造擬基本解並研究其性質與套用方面，擬微分運算元與傅立葉積分運算元有著根本的作用。

配圖

相關連線