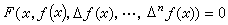有限差方程
正文
含有未知函式的差分的條件等式,它是重要的一類函式方程,也稱有限差分方程。有限差方程的一般形式是
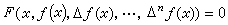 , (1)
, (1)
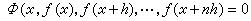 。 (2)
。 (2)
滿足有限差方程的函式稱為它的解,n階有限差方程的含有 n個任意常數的解稱為通解。通解中的任意常數被確定後,即可獲得一個特解。
線性有限差方程解的結構 稱有限差方程
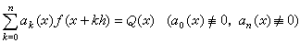 , (3)
, (3)
方程(3)的解具有以下性質:① 如果函式ƒ1(x),ƒ2(x),…,ƒn(x)是相應於方程(1)的齊次方程的線性無關解,則相應的齊次方程的通解為
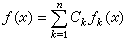 ,其中C1,C2,…,Cn為任意常數。②方程(3)的通解可表為它的一個特解 ƒ*(x)與相應的齊次方程的通解之和,即
,其中C1,C2,…,Cn為任意常數。②方程(3)的通解可表為它的一個特解 ƒ*(x)與相應的齊次方程的通解之和,即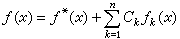 ,這兩條性質就完全確定了線性有限差方程解的結構。
,這兩條性質就完全確定了線性有限差方程解的結構。 常係數線性有限差方程 如果方程(3)中的αk(x)(k=0,1,…,n)都為常數,且h=1,則方程
 (4)
(4)
求得方程(4)的通解,可根據線性有限差方程解的結構特點,由以下兩個步驟來完成。第一步,求相應於(4)的齊次方程
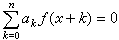
 ,
,
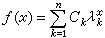 :如果特徵根中有實的重根出現,則齊次方程的通解為
:如果特徵根中有實的重根出現,則齊次方程的通解為  ,
,
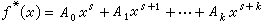 ,代入方程(4),兩邊對比係數,可求出待定係數A0,A1,…,Ak,從而求得方程(4)的一個特解ƒ*(x)。又如Q(x)=p(x)b)x,其中p(x)為k次多項式,k為特徵方程的s重根,則設
,代入方程(4),兩邊對比係數,可求出待定係數A0,A1,…,Ak,從而求得方程(4)的一個特解ƒ*(x)。又如Q(x)=p(x)b)x,其中p(x)為k次多項式,k為特徵方程的s重根,則設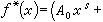
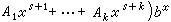 , 代入方程(4),求出待定係數,即得方程(4)的一個特解。將兩步所求得的結果相加,即可得到方程(4)的通解。
, 代入方程(4),求出待定係數,即得方程(4)的一個特解。將兩步所求得的結果相加,即可得到方程(4)的通解。 如果特徵根中出現復根,則對每一對共軛復根,利用歐拉公式
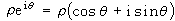 ,分別取實部和虛部作為線性無關解,參照上述方法,也可得到實的通解
,分別取實部和虛部作為線性無關解,參照上述方法,也可得到實的通解 除去上述的解法,還可利用發生函式、符號運算元以及變易常數等方法去求方程(4)的通解。
舉例 求二階常係數線性有限差方程
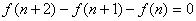 ,
,
相應的特徵方程為 λ2-λ-1=0。由此解出特徵根為
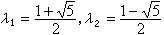 。從而通解為
。從而通解為 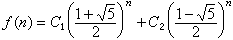 ,
,
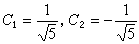 。故解為
。故解為 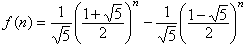 。
。
參考書目
L.M.Milne-Thomson,The Calculus of Finite Differences, Macmillan, London,1951.