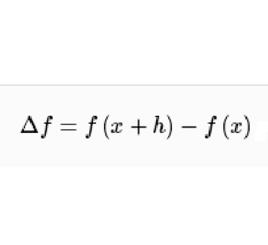基本概念
差分運算元在數值積分、數值微分和微分方程的數值解中是很有用的。人們總是希望把非平穩時間序列變換成平穩序列,以便於用數學方法來處理,而最常用的變換是差分變換。
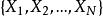 差分運算元
差分運算元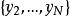 差分運算元
差分運算元 差分運算元
差分運算元對於序列 ,其 一階(向後)差分(first-order (backward) difference)定義為 ,這裡 。
二階差分(second-order difference)定義為
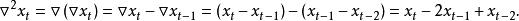 差分運算元
差分運算元類似地, p階差分為:
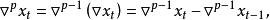 差分運算元
差分運算元s期滯後差分為:
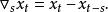 差分運算元
差分運算元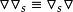 差分運算元
差分運算元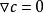 差分運算元
差分運算元顯然, ;對於常數c,。
相關概念
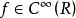 差分運算元
差分運算元假定所討論的函式都是無窮次可微分的實函式, ,令h表示函式自變數的最小增量,定義運算元:
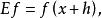 差分運算元
差分運算元位移運算元:
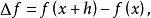 差分運算元
差分運算元向前差分運算元:
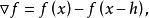 差分運算元
差分運算元向後差分運算元 :
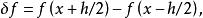 差分運算元
差分運算元中心差分運算元:
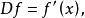 差分運算元
差分運算元微分運算元:
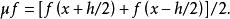 差分運算元
差分運算元平均運算元:
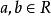 差分運算元
差分運算元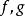 差分運算元
差分運算元這些運算元都是線性的,因為下列等式對於任意的常數 和函式 皆成立:
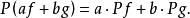 差分運算元
差分運算元任意兩個線性運算元 P與 Q的和、積、冪由下列等式定義:
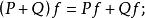 差分運算元
差分運算元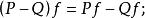 差分運算元
差分運算元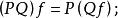 差分運算元
差分運算元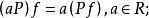 差分運算元
差分運算元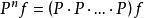 差分運算元
差分運算元,n個因子.
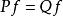 差分運算元
差分運算元 差分運算元
差分運算元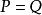 差分運算元
差分運算元當 對於一切函式 皆成立時,兩個運算元 P,Q為相等,即 。
差分運算元的若干性質
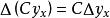 差分運算元
差分運算元(1) (C為常數);
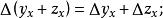 差分運算元
差分運算元(2)
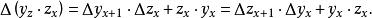 差分運算元
差分運算元(3)
套用舉例
Taylor級數
利用運算元,由通常的形式
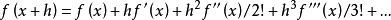 差分運算元
差分運算元得出
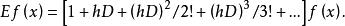 差分運算元
差分運算元(1)
指數函式
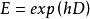 差分運算元
差分運算元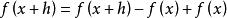 差分運算元
差分運算元等式(1)中方括弧里的式子是運算元 hD的指數函式 的冪級數展開式,由恆等式 得到下列關係:
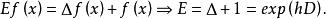 差分運算元
差分運算元二項式定理
向前差分運算元的二次冪:
 差分運算元
差分運算元即
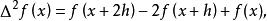 差分運算元
差分運算元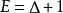 差分運算元
差分運算元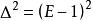 差分運算元
差分運算元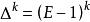 差分運算元
差分運算元使人想到二項式定理。由 得 ,對於任意的冪次,有等式 。