正文
人口控制論研究人口系統結構和參數的變化，分析人口系統的特性和動態行為，其目的是通過調節和控制生育率來改變和控制人口發展趨勢，從而使人口系統的繁衍過程朝著人們期望的方向發展。人口控制論的研究對於象中國這樣大力提倡計畫生育和實行人口控制的國家尤為重要。發展狀況 人口學歷來被認為是純屬於社會科學的範疇，但也可以從自然科學角度來研究它。20世紀70年代初，美國的D.R.福爾肯伯格、G.J.奧爾斯德、H.L.朗哈爾、荷蘭的H.夸克納克和日本的高橋安等人，開始套用控制論方法研究人口問題。70年代末中國控制論科學家宋健從理論和套用兩個方面對人口控制進行了系統的定量研究，在數學模型、人口指數、人口系統動態分析、穩定性理論、人口預報、人口結構和人口發展過程的最優控制等方面都取得了很多重要結果，奠定人口控制論的理論基礎。人口控制論已套用於中國人口控制的實踐中。
人口系統數學模型 人口控制論的首要任務是建立人口系統的數學模型（見人口系統數學模型）。人口系統的定量理論研究、計算機仿真和數值計算都是以人口系統數學模型為基礎的。
人口系統動態分析 主要研究人口系統在給定輸入下的過渡過程、時間常數、通頻帶，以及人口狀態類型和狀態轉換等。人口系統不同於一般工程系統，它的時間常數接近於人的平均期望壽命。人口狀態在離散模型中是指社會人口中各年齡組的數量分布，可表示為向量
，式中分量
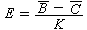是t年代滿i周歲的人數。圖1中以人口平均密度
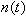（總人口除以平均壽命的數值）和平均壽命s0為基準，以年齡i為橫坐標表示出6種人口狀態類型。①穩態型:特點是i小於s0的各年齡組人數都小於並接近n(t)。在自然增長率很小的國家中,如西歐和北歐,人口狀態均接近穩態型。②增長型：各年齡組的人數隨年齡減少而增加。在大多數自然增長率大的國家中，人口狀態屬於這種類型。③下降型：小於s0的各年齡組的人數大部分隨年齡減小而減小。④峰型：小於平均壽命的某一年齡區間的各組人數顯著超過基準值n(t)，達到n(t)的1.5倍以上者稱為強峰型。峰型、特別是強峰型人口狀態可能對社會經濟生活產生嚴重影響。圖2是1978年中國年齡分布曲線,在0～18歲和19～30歲分別有兩個峰，約為n(t)的1.5～2倍。⑤谷型：在某一年齡區間各年齡組人數顯著小於n(t)，這說明由於某種社會因素使這些年齡組在過去某些年代死亡率很高，它與峰型一樣會帶來不利的影響。⑥振盪型：在小於平均壽命的區間有二個以上的脈衝式峰和谷相間出現，它的不利影響比脈衝式單峰或單谷更為嚴重，是應該盡力避免的。 
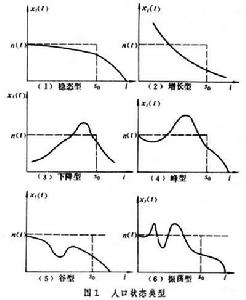人口控制論
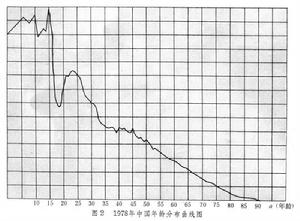人口控制論人口系統穩定性理論 人口系統是一個帶有正反饋的動態系統，因而存在著李雅普諾夫穩定性問題。在人口控制論中，宋健等人用半群理論首次證明，對於任一定常人口系統（見定常系統），都存在一臨界婦女總和生育率βcr：
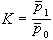
人口系統的能控性和能觀測性 人口系統的能控性問題就是社會能否通過控制婦女生育率來控制人口系統的繁衍過程，即在一定條件下用適當的政策、法律或其他措施對人口系統的演化加以控制的可能性。如果婦女總和生育率β(t)的取值範圍為【βm，βM】，那么人口系統能控的充分必要條件為βm＜βcr和βM＞βcr。這個條件表示,人口系統的能控性既與臨界婦女生育率有關,也與作為控制變數的婦女總和生育率β(t)的取值範圍有關。人口系統的能觀測性問題，是指能否根據人口系統的輸出唯一地確定初始人口狀態。所有各項人口指數都是人口系統的觀測量，它們可從人口普查或抽查中得到。在人口統計中為了獲得某一年的人口年齡分布，需要進行人口普查，這是一件很複雜的工作。但某一項或幾項人口指數的統計可能比較容易。如果能根據這幾項人口指數的統計來確定人口狀態,便可簡化人口統計工作,這對於人口統計學具有重要意義。
人口系統參數估計和辨識 系統辨識能用於估計和辨識人口系統的參數和模型。這些參數包括死亡率、嬰兒死亡率、生育率、生育模式、遷移模式等。
人口系統參數的靈敏度分析 人口系統參數的變化（確定性的或隨機性的）對人口系統巨觀性能的影響是不一樣的，系統對有些參數如死亡率、生育率是很敏感的；對有些參數如生育模式、女性比例函式，系統是不敏感的。對這些問題的精細研究，有利於設定人口預測時的參數和處理人口統計數據。
人口系統的預測理論 在作人口發展預測時利用人口系統數學模型，根據初始年代的人口狀態確定各項人口參數，在計算機上求解人口發展方程，便可求出今後任何一年的人口狀態和各項人口指數。這些數據是人口政策的重要參考依據。人口發展的預測對制定人口政策、人口規劃以及國民經濟規劃都是非常重要的。人口系統是一個慣性很大的動態系統，系統輸出對輸入的反應很慢，時間常數等於其平均壽命，約70～80年的時間。這個特點的社會意義是：一種人口政策對人口系統的影響要經過很長時間才能顯示出來。到了那個時候，如果時間證明政策錯了，即使想要糾正它也已為時過晚，不得不承擔這一切後果的將是子孫後代，而他們要想糾正這一錯誤還要付出更大的時間代價。因此，對於象人口這樣慣性很大的社會系統來說，預測具有特別重要的意義。
人口目標 每一個社會的生態系統和自然資源對人口的負載能力存在一個有窮的極限。因此人類社會應該為人口的增長規定一個限度。一個國家或社會的人口數量不能無限增多也不能逐步減少到種族滅絕，因此在人類文明發展的每一個歷史時期必然存在一個適中的人口數量，以便同社會的經濟發展水平、自然資源的多寡以及生態系統的負載能力保持平衡。不斷地研究和確定每一個國家或社會的適中人口數量，就是人口目標問題。
人口系統最優控制理論 把一個國家的現有人口調整並穩定在人口目標值附近，就是人口控制問題，又稱為人口過渡問題。這一過渡是通過調節婦女生育率來實現的，可以用最優控制理論來解決。若用N*表示將來的人口目標，則由N*唯一確定相應人口狀態x*。通過婦女總和生育率β(t),把人口系統從給定的初態 x0在有限時間T內（T不是固定的）控制到理想狀態x*。作為控制變數的總和生育率β(t)的取值範圍是U＝【β1,β2】。除了控制約束外，還應考慮到人口系統社會因素方面的限制。例如,在控制過程中，人口總數峰值不能太大,社會撫養指數不能過高，人口老化不能太嚴重等。所有這些限制實質上是對人口狀態的約束。所有滿足這些約束的人口狀態集合用Q(t)表示。性能指標的選擇不是唯一的，一種比較自然的選擇是
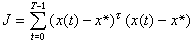$$
!! 其中x(t)是受控過程中的人口狀態，τ表示向量轉置。因此人口系統最優控制可以描述為在給定人口目標N*後，希望尋求最優婦女總和生育率
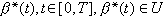。在β*(t)的控制下,使人口系統從初態x0轉移到理想狀態x*。在控制過程中，人口狀態x(t)∈Q(t)，且使性能指標J取極小值。這樣求出的 β*(t)就是人口系統的最優控制,它也是人口發展的長、中、短期的最優規劃。圖3是中國未來人口不超過12億、撫養指數不超過1.0和老化指數不超過0.7的最優控制計算結果。圖中N(t)是人口總數（10億）。 
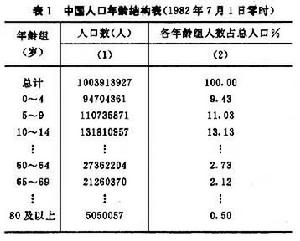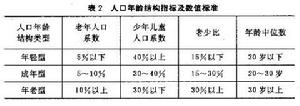人口控制論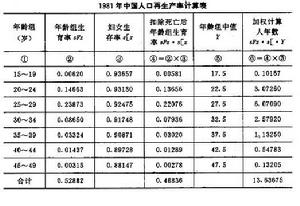
人口控制論
人口控制論參考書目
宋健、於景元著：《人口控制論》，科學出版社，北京，1985。
