簡介
兩個連線埠中接電源的稱為入口,接負載的稱為出口。連線埠上的電壓V1、V2和電流i1、i2分別稱為連線埠電壓和連線埠電流,又統稱為連線埠變數。
說明
二連線埠網路有無源和有源、線性和非線性、時不變和時變之分,它既可能是一個異常複雜的網路,也可能是相當簡單的網路。變壓器、放大器等的電路模型都可歸結為雙口網路。在電路圖上,二連線埠網路可統一表達成圖中所示形式。表達4個連線埠變數之間關係的方程稱為二連線埠網路方程。
同一個二連線埠網路可以有6組不同形式的方程。其矩陣形式與多端網路的約束關係類似。6組方程右端變數前的4個係數稱為二連線埠網路的參數,共6組,分別稱為短路導納參數 、開路阻抗參數、第一類混合參數、第二類混合參數、傳輸參數和反向傳輸參數。6組參數都可用來表征二連線埠網路。對於一個網路究竟選用哪一組參數,視具體情況而定。
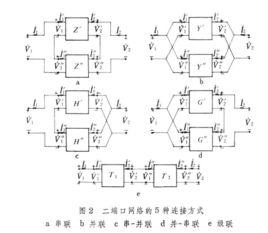
 二連線埠網路
二連線埠網路電子電路中會經常遇到二連線埠網路的相互連線。它們之間的連線有5種方式,分別為串聯、並聯、串-並聯、並-串聯和級聯。這樣連線而成的網路仍為二連線埠網路。例如,電力系統中用於模擬遠距離輸電線的鏈型電路就是一些二連線埠網路級聯而成的。
方程和參數
表達4個連線埠變數之間關係的方程稱為二連線埠網路方程。同一個二連線埠網路可以有 6組不同形式的方程。對於一個不含電源並處於正弦穩態的線性時不變網路,這6組方程如表1所示。位於每組方程右端變數前的 4個係數稱為二連線埠網路的參數,共6組,並按所在之方程而被分別命名為短路導納參數(或Y 參數)、開路阻抗參數(或Z 參數)、第一類混合參數(或H 參數)、第二類混合參數(或G 參數)、傳輸參數(或T參數)和反向傳輸參數(或T'參數)。
這6組參數組成的6個參數矩陣,依次稱為短路導納矩陣、開路阻抗矩陣、第一類混合矩陣、第二類混合矩陣、傳輸矩陣和反向傳輸矩陣,並分別記為尯、屇、媨、媠、寭 和T'。另外,6組參數中每個參數自身都有特定的物理含義。例如
由此4式可知: Y11是連線埠2短路(妭2=0)時連線埠1的策動點導納; Y12是連線埠1短路( V1=0)時連線埠1對連線埠2的轉移導納; Y21是連線埠2短路(妭2=0)時連線埠2對連線埠1的轉移導納; Y22是連線埠1短路(妭1=0)時連線埠2的策動點導納。當確定連線埠1是入口、連線埠2是出口後, Y12是反向轉移導納, Y21是正向轉移導納。用類似的方法,可對其他參數作出相應的解釋。
6組參數都可用來表征二連線埠網路。 對於一個網路究竟選用哪一組,視具體情況而定。例如晶體三極體的 H參數易於測定,所以該管的等效二連線埠網路多用 H參數來表征。另外,也並非每個二連線埠網路都具有6類參數,例如理想變壓器便既無 Y參數,也無 Z參數。
當 Y12= Y21(或 Z12= Z21, H12=- H21, G12=- G21, A D- B C=1, A┡ D┡- B┡ C┡=1)時,二連線埠網路具有互易性質。具有互易性質的二連線埠網路的每類參數中只有 3個參數是獨立的。
 二連線埠網路
二連線埠網路 二連線埠網路
二連線埠網路二連線埠網路的非同類參數可以相互換算。表2所列為常用的 Y 參數、 Z 參數、 H參數、 T 參數之間的換算關係。
連線
 二連線埠網路
二連線埠網路按圖2所示的5種方式連線在一起。這5種方式分別稱為串聯、並聯、串-並聯、並-串聯和級聯。如此連線而成的網路仍然是一個二連線埠網路。在兩個二連線埠網路的連線埠電流約束條件不遭受破壞的限制下,對串聯而成的總二連線埠網路有Z=Z┡+Z"上式表明,總二連線埠網路的開路阻抗矩陣等於原有兩個二連線埠網路的開路阻抗矩陣之和。類似地,對其餘4種連線方式依次有: Y=Y┡+Y";H=H┡+H";G=G┡+G"和T=T1·T2。
在電子電路中會經常遇到二連線埠網路的相互連線。例如,帶負反饋的放大電路就是由一個二連線埠網路(基本放大器)和另一個二連線埠網路(反饋網路)根據反饋方式或串聯、或並聯、或串-並聯、或並-串聯而成的;多級放大電路和濾波電路則是一些二連線埠網路級聯而成的。在電力系統中用來模擬遠距離輸電線的鏈型電路也是一些二連線埠網路(T型網路或劧型網路)級聯而成的。
 二連線埠網路
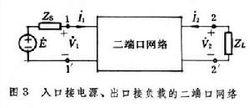
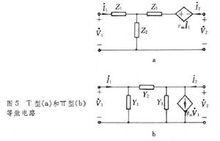
二連線埠網路有載二連線埠網路的輸入阻抗和輸出阻抗 當二連線埠網路的入口即連線埠1-1┡接有內阻抗為Zs的電源,出口即連線埠2-2┡接有阻抗為ZL的負載時(圖3),入口處的電壓妭1與電流夒1之比為該網路的輸入阻抗(或策動點阻抗)Zi;負載阻抗ZL=∞(出口開路)時的出口電壓V20與負載阻抗ZL=0(出口短路)時的出口電流-夒2s 之比為該網路的輸出阻抗Z0。
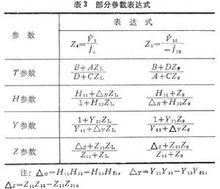
利用二連線埠網路方程,再配以電源支路方程和負載支路的方程,可以導出用各種參數和ZL表達的Zi及用各種參數和Zc表達的Z0。 其中的部分表達式見表3。
輸入阻抗是對連線埠1-1┡而言的。當把電源接在連線埠2-2┡上,把負載接在連線埠1-1┡上(此時是連線埠2-2┡作為入口,連線埠1-1┡作為出口),還可得出對連線埠2-2┡而言的輸入阻抗Z┡i,其用T 參數的表達式
在ZL=∞和ZL=0兩種極端情況下,有 和 Zi10和Zi20分別稱為連線埠 1-1┡和連線埠2-2┡的開路輸入阻抗(開路策動點阻抗);Zi1s和Zi2s分別稱為連線埠1-1┡和連線埠2-2┡的短路輸入阻抗(短路策動點阻抗)。
這 4個阻抗之間存在如下的關係,即 上式說明它們之中只有3個是獨立的。 已知互易二連線埠網路的T參數 A、B、C、D滿足等式AC-BC=1,於是,通過求解由此等式和任意3個上述阻抗表達式共同組成的方程組, 便可得出該網路的全部T 參數;再通過參數間的換算公式可以求出其他各類參數。開路阻抗和短路阻抗最容易測定,所以對互易二連線埠網路的 6類參數的測定可通過測定這二種阻抗來實現,而且只要測定出4個阻抗中任意3個即可。
 二連線埠網路
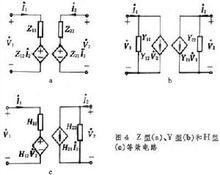
二連線埠網路二連線埠網路的等效電路 圖4上的電路是二端品網路的3個等效電路,因為它們的外特性方程恰好依次是二連線埠網路的Z型、Y型和H型方程。圖5上的T型電路和劧型電路也可作為等效電路,但要求:T型電路中阻抗和受控電源的控制係數 (γm)與二連線埠網路的Z參數間應有關係 Z1=Z11-Z12 Z2=Z12Z3=Z22-Z12 γm=Z21-Z12劧型電路中的導納和受控電源的控制係數 (gm)與二連線埠網路的Y參數間應有關係 Y1=Y11+Y12 Y2=-Y12 Y3=Y22+Y12 gm=Y21-Y12互易二連線埠網路的等效 T型電路和劧型電路皆不含受控電源,因為此時Z12=Z21和Y12=Y21使γm=0和gm=0。
互易二連線埠網路
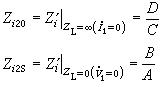 二連線埠網路公式
二連線埠網路公式介紹
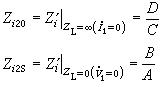 二連線埠網路公式
二連線埠網路公式互易二連線埠網路,為二連線埠網路的一種特殊情況,即原網路中無獨立電源,無受控電源等耦合元件和所有動態元件初始條件置零。如果Z11=Z22,則成為對稱互易雙口網路。其兩個連線埠可不加區別,無論從哪個連線埠看過去,其電氣性能是完全相同的。
參數
 二連線埠網路
二連線埠網路根據互易定理,互易雙口網路滿足:
Z參數:Z12=Z21;
Y參數:Y12=Y21;
H參數:h12=-h21;
T參數:ΔT=1;
G參數:g12=-g21;
T'參數:ΔT'=1。