基本簡介
 三體問題
三體問題N體問題:N體問題可以用一句話寫出來:在三維空間中給定N個質點,如果在它們之間只有萬有引力的作用,那么在給定它們的初始位置和速度的條件下,它們會怎樣在空間中運動。
三體問題:最簡單的例子就是太陽系中太陽,地球和月球的運動。在浩瀚的宇宙中,星球的大小可以忽略不及,所以我們可以把它們看成質點。如果不計太陽系其他星球的影響,
那么它們的運動就只是在引力的作用下產生的,所以我們就可以把它們的運動看成一個三體問題。
天體力學中的基本力學模型。研究三個可視為質點的天體在相互之間萬有引力作用下的運動規律問題。這三個天體的質量、初始位置和初始速度都是任意的。在一般三體問題中,每一個天體在其他兩個天體的萬有引力作用下的運動方程都可以表示成3個二階的常微分方程,或6個一階的常微分方程。因此,一般三體問題的運動方程為十八階方程,必須得到18個積分才能得到完全解。然而,目前還只能得到三體問題的10個初積分,還遠不能解決三體問題。
研究起源
 三體問題
三體問題為了說明他的觀點,希爾伯特
 三體問題
三體問題費爾馬猜想經過全世界幾代數學家幾百年的努力,終於在1993年被中國的數學家毛桂成用費爾馬的絕妙證明方法最終解決,這被公認為二十世紀最偉大的數學進展之一,因為除了解決一個重要的問題,更重要的是在解決問題的過程中好幾種全新的數學思想誕生了,難怪在問題解決後也有人遺憾地感嘆一隻會生金蛋的母雞被殺死了。
英國數學家安德魯.懷爾斯是用無理數方程作假證明的費爾馬猜想,無理數中根本就沒有一個整數存在,故無整數解存在,但他沒有證明整數中有沒有一組數使費爾馬大定理成立。
他用無理數公式證明的費爾馬大定理的證明方法是錯的,只能用整數公式證明費爾馬大定理。費爾馬的絕妙證明方法就是用整數公式證明的費爾馬大定理。
研究方法
 三體問題
三體問題第一類是分析方法,其基本原理是把天體的坐標和速度展開為時間或其他小參數的級數形式的近似分析表達式,從而討論天體的坐標或軌道要素隨時間的變化;
第二類是定性方法,採用微分方程的定性理論來研究長時間內三體運動的巨觀規律和全局性質;
第三類是數值方法,這是直接根據微分方程的計算方法得出天體在某些時刻的具體位置和速度。這三類方法各有利弊,對新積分的探索和各類方法的改進是研究三體問題中很重要的課題。
數學推斷
 三體問題
三體問題m1(d2 q1i/dt2)= k m1 m2 /(q2i - q1i)(R312) + km1 m3 /(q3i - q1i)(r313)
m2(d2 q2i/dt2)= k m2 m1 /(q1i - q2i)(r321) + km2 m3 /(q3i - q2i)(r323)
m3(d2 q3i/dt2)= k m3 m1 /(q1i - q3i)(r331) + km3 m2 /(q2i - q3i)(r332)
( i =1,2,3 )其中m i 是質點的質量,k 是萬有引力常數,r ij 是兩個質點m i 和m j 之間的距離,而 q i1 , q i2 , q i3 則是質點 m i 的空間坐標。所以三體問題在數學上就是這樣九個方程的二階常微分方程組再加上相應的初始條件。(事實上根據方程組本身的對稱性和內在的物理原理,方程可被簡化以減少變數個數)。而N體問題的方程也是類似的一個 N2 個方程的二階常微分方程組。 當 N=1 時,單體問題是個平凡的方程。
單個質點的運動軌跡只能是直線勻速運動。當 N=2 的時候 (二體問題),問題就不那么簡單了。但是方程組仍然可以化簡成一個不太難解的方程,任何優秀的理科大學生大概都能輕易解出來。簡單來說這時兩個質點的相對位置始終在一個圓錐曲線上,也就是說如果我們站在其中一個質點上看另一個質點,
那么另一個質點的軌道一定是個橢圓,拋物線,雙曲線的一支或者直線。二體問題又叫克卜勒(Johannes Kepler)問題,它是在1710年被瑞士數學家約翰伯努利(Johann Bernoulli) 首先解決的。N體問題的提出大概可以追溯到上千年前,但是這一問題的第一個完整的數學描述(象使用上面這樣的微分方程)是出現在牛頓的“自然哲學的數學原理”(Philosophiae Naturalis Prinicipia Mathematica,1687年出版)一書中。在他的著作中,牛頓成功地運用微積分證明了克卜勒的天文學三大定律,但是奇怪的是他的書里並沒有給出二體問題的解,儘管這兩者是緊密相關的,而且現在的人們還是相信牛頓當時完全有能力自己給出二體問題的解。至於三體問題或者更一般的N體問題(N大於二),在被提出以後的二百年里,被十八和十九世紀幾乎所有著名的數學家都嘗試過,但是問題的進展是微乎其微的。儘管在失敗的嘗試中微分方程的理論被不斷地發展成為一門更成熟的數學分支,但是對於這些發展的源頭——N體問題,人們還是知道的太少了。終於在十九世紀末期,也就是希爾伯特做他的著名演講前幾年,人們期待的重大突破出現了。
特殊情況
 三體問題
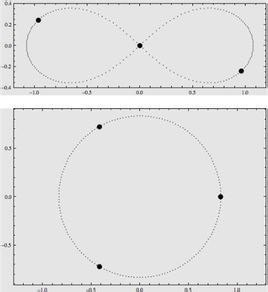
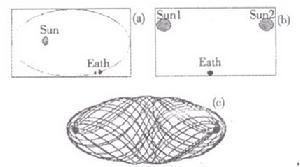
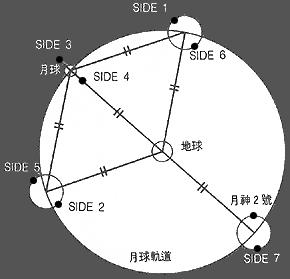
三體問題1、三星成一直線,邊上兩顆圍繞當中一顆轉。
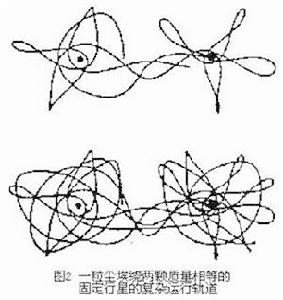
2、三星成三角形,圍繞三角形中心鏇轉。
3、兩顆星圍繞第三顆星鏇轉。
4、三個等質量的物體在一條8字形軌道上運動。
限制性三體問題
三體問題的特殊情況。當所討論的三個天體中,有一個天體的質量與其他兩個天體的質量相比,小到可以忽略時,這樣的三體問題稱為限制性三體問題。一般地把這個小質量的天體稱為無限小質量體,或簡稱小天體;把兩個大質量的天體稱為有限質量體。 把小天體的質量看成無限小,就可不考慮它對兩個有限質量體的吸引,也就是說,它不影響兩個有限質量體的運動。於是,對兩個有限質量體的運動狀態的討論,仍為二體問題,其軌道就是以它們的質量中心為焦點的圓錐曲線。根據圓錐曲線為圓、橢圓、拋物線和雙曲線等四種不同情況﹐相應地限制性三體問題分四種類型:圓型限制性三體問題﹑橢圓型限制性三體問題﹑拋物線型限制性三體問題和雙曲線型限制性三體問題。若小天體的初始位置和初始速度都在兩個有限質量體的軌道平面上,則小天體將永遠在運動。爾按限制性三體問題研究月球的運動,略去太陽軌道偏心率﹑太陽視差和月球軌道傾角,實際上這就是一種特殊的平面圓型限制性三體問題。他得到的周期解,就是希爾月球運動理論的中間軌道。 在小行星運動理論中,常按橢圓型限制性三體問題進行討論,脫羅央群小行星的運動就是太陽-木星-小行星所組成的橢圓型限制性三體問題的等邊三角形解的一個實例。布勞威爾還按橢圓型限制性三體問題來討論小行星環的空隙。拋物線型限制性三體問題和雙曲線型限制性三體問題在天體力學中則用得很少。人造天體出現後,限制性三體問題有了新的用途,常用於研究月球火箭和行星際飛行器運動的簡化力學模型,見月球火箭運動理論和行星際飛行器運動理論)。
研究趣聞
 三體問題
三體問題三體問題和瑞典國王的獎金(奧斯卡國王——米塔格萊夫勒——龐加萊) 1885年,在剛創刊不久的瑞典數學雜誌Acta Mathematica的第七卷上出現了一則引人注意的通告:為了慶祝瑞典和挪威國王奧斯卡二世在1889年的六十歲生日,Acta Mathematica將舉辦一次數學問題比賽,懸賞2500克郎和一塊金牌。
而比賽的題目有四個,其中第一個就是找到N體問題的所有解。參加比賽的各國數學家必須在1888年的6月1日前把他們的參賽論文寄給雜誌的創辦人和主編,著名的瑞典數學家米塔格萊夫勒(GostaMittag-Leffler)。所有論文將被匿名地被一個國際委員會評判以決出優勝者,然後優勝者的論文將發表在Acta Mathematica上。這個委員會由三個當時赫赫有名的數學家組成:德國的維爾斯特拉斯(Karl Weierstrass),法國的赫密特(Charles Hermite)和米塔格萊夫勒本人組成。 從現代的觀點來看,這樣的比賽也許有“抄作”和給新雜誌做廣告的嫌疑。(事實上當時就有一些數學家這樣批評這種比賽,象德國的克隆奈克(Leopold Kronecker))。但是從歷史上看,米塔格萊夫勒和奧斯卡二世的動機是好的,是為了推動科學的發展。奧斯卡二世本人在大學中數學就學得很好,他和許多當時著名的數學家,象維爾斯特拉斯,科瓦列夫斯卡雅(Sonya Kovalevskaya)等都有親密的關係。而米塔格萊夫勒更是雄心勃勃,想把這樣的比賽每四年舉行一次。可惜這個構想沒有實現,比賽只舉辦了一次就夭折了,否則的話也許今天數學的最大獎不是菲爾茲(John Charles Fields)獎而是奧斯卡獎了(那樣後來美國的電影獎大概也要考慮換個名字了)。
回到比賽本身。這次比賽在當時轟動一時,雖然獎金不高,這種崇高的榮譽是當時罕見的,要知道瑞典更有名的“炸藥獎”諾貝爾(Alfred Bernhard Nobel)獎是在幾年後的1896年才開始評選的。但是由於問題的困難程度,大多數一開始躍躍欲試的數學家後來都知難而退,最後只有四五個數學家真正交了他們的答卷。而優勝者也並不難選出,雖然還是沒有人能完整地解決任何一個問題,但是所有評審一致認為其中一份答卷對於N體問題的解決做出了關鍵的貢獻,應該把獎頒給這位數學家。這位獲勝者就是法國數學家,物理學家龐加萊(Jules Henri Poincare)。 龐加萊在現代數學歷史上占有舉足輕重的地位,他曾被稱為現代數學的兩個奠基人之一(另一個是黎曼(Bernhard Riemann)),也有人稱他為歷史上精通當時所有數學的最後兩個人之一(另一個就是希爾伯特))。
而1885年的龐加萊只有31歲,雖然已初露鋒芒,但還是一位希望能夠一舉成名的年輕數學家,所以這次比賽是個大好的機會,這也迫使他先放下手上其他的工作,集中精力投入到天體力學和N體問題的研究中。龐加萊獲獎的論文“關於三體問題的動態方程”(Sur le probleme des trois corps et les equations de la dynamique) 最後在1890年在Acta Mathematica上發表,論文長達270頁,占了整整半卷雜誌。 這篇重要論文使原來就已有不小名氣的年輕龐加萊更加譽滿整個歐洲數學界,也使他得到了新的熱情和動力繼續進行他在這篇論文中開始的工作。從1892年到1899年,龐加萊陸續出版了他的三大卷宏偉巨著“天體力學的新方法”(Les MethodsNouvelles de la Mecanique Celeste)。他的獲獎論文和這三卷書可以說奠定了現代天體力學,動力系統,微分方程定性理論,甚至混沌理論的基礎,儘管大多數他的思想直到幾十年後才被廣大的數學工作者所領悟進而發展成現代的數學理論。