三垂定理也叫三垂線定理。
內容:如果一條斜線在一個平面內的射影與該平面的某條直線垂直,則這條斜線也與該直線垂直。
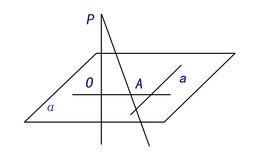
如圖所示,平面內的一條直線,如果與穿過這個平面的一條斜線在這個平面上的射影相垂直垂直,那么它也和這條斜線垂直。又稱為三垂線定理。
三垂定理也叫三垂線定理。
內容:如果一條斜線在一個平面內的射影與該平面的某條直線垂直,則這條斜線也與該直線垂直。
垂徑定理是數學幾何(圓)中的一個定理,它的通俗的表達是:垂直於弦的直徑平分弦且平分這條弦所對的兩條弧。數學表達為:如圖,直徑DC垂直於弦AB,則AE=E...
定理定義 數學證明 推導定理 定理簡史 定理意義三垂線定理指的是平面內的一條直線,如果與穿過這個平面的一條斜線在這個平面上的射影垂直,那么它也和這條斜線垂直。
簡介 定理證明 三餘弦定理 使用 用途數學定理列表(按字母順序排列) 以下列出了許多數學定理,供查閱與引用。
三割線定理是調和點列中的一個熟知結論,卻曾被民間數學家多次"發現".三割線定理可表述為:PAB、PCD為⊙O的兩任意割線,AD與BC交於Q,PQ交⊙O於...
證法1 證法2《國中數理化公式定理大全》是2009年龍門書局出版社出版的圖書,作者是安學典。本書收錄了國中數學物理化學的概念、公式、定理。
圖書信息 常見數學定理幾何定理,屬於數學領域。分為平面幾何、解析幾何。具體事例有勾股定理 餘弦定理。條目分為立體幾何,三角形的六心以及重要定理等。
簡介 條目圓心角定理,英文名為(The center angle theorem)。常用於數學計算,其主要功能用來計算相關圓的弧長問題。
定理內容 推理過程 相關內容三角形的三條高交於一點。該點叫做三角形的垂心。
概述 其性質包括垂極點是當D、E、F是三角形ABC三點在任一直線L上的投影,則D、E、F到對邊BC、AC、AB的垂線共點,這個點即是。
定義 研究