電磁場的格林函式
正文
線上性媒質中,任意分布的簡諧(或穩恆)源所激勵的場,都可以化為單位點源所激勵的場的線性組合。在確定的媒質和邊界條件下,單位點源所激勵的場矢量或勢函式就稱為該條件下場或勢的格林函式。它們是場點位置矢徑r和源點位置矢徑r′的函式。電磁場邊值問題的解可以表示成源函式與格林函式乘積的積分。標量格林函式 在均勻無界媒質中,自由電荷密度ρ 所產生的標勢φ在洛倫茲規範下滿足方程
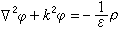 (1)
(1)
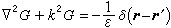 (2)
(2)
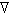 2對r點的坐標作運算,δ(r -r′)是集中作用在r′點的狄拉克δ-函式。此方程的解是
2對r點的坐標作運算,δ(r -r′)是集中作用在r′點的狄拉克δ-函式。此方程的解是 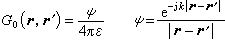 (3)
(3)
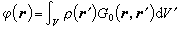 (4)
(4)
 (5)
(5)
如果均勻媒質空間V被閉曲面S0所包圍,套用格林第二公式,並利用格林函式的對稱性 G(r′,r)=G(r,r′),可得
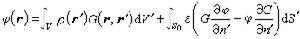 (6)
(6)
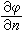 或
或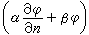 的邊界值時,應相應地規定
的邊界值時,應相應地規定 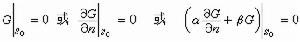
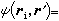
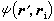 以及對於S上的源點ri=r,有
以及對於S上的源點ri=r,有 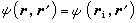 和
和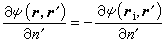
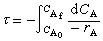 (7)
(7)
設在r′點放置的電流源J, 它的三個分別沿正交單位矢量e媴(i=1,2,3)的電偶極矩為
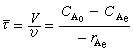 (8)
(8)
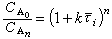 (9)
(9)
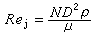 (10)
(10)
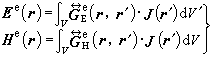 (11)
(11)
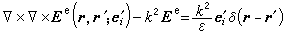 (12)
(12)
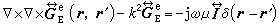 (13)
(13)
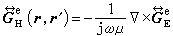 (14)
(14)
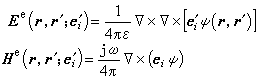 (15)
(15)
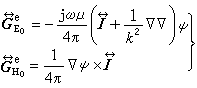 (16)
(16)
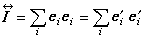 是單位並矢,
是單位並矢, 當r →r′時,Ee為|r →r′|-3的量級,所以當J(r)厵0時,
 在數學上不收斂,應當取其主值。因此,一般應使
在數學上不收斂,應當取其主值。因此,一般應使 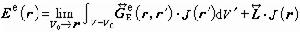 (17)這裡V0是包含r 點的某種形式的微體積;
(17)這裡V0是包含r 點的某種形式的微體積;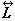 是一個並矢,V0→r表示V0全部的點趨近於r點。
是一個並矢,V0→r表示V0全部的點趨近於r點。 同樣,還可以規定另一對磁並矢格林函式
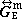 和
和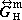 ,它們對應了沿e媴方向的磁偶極矩所產生的電磁場Em(r,r′;ei)和Hm(r,r′;e媴),並有關係式
,它們對應了沿e媴方向的磁偶極矩所產生的電磁場Em(r,r′;ei)和Hm(r,r′;e媴),並有關係式 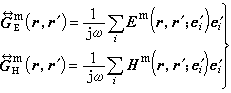 (18)
(18)
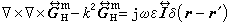 (19)
(19)
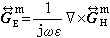 (20)
(20)
P.M. Morse and H. Feshback,Methods of Theoretical physics,McGraw-Hill,Inc.,New York,Kōgakusha Co.,Ltd.Tokyo,1953.
C. T. Tai,Dyadic Green's Functions in Electromagnetic Theory ,Intext Educational Pub.,Scranton,1971.
