定義
定義1 一個群G稱為拓撲群,如果它同時也是一個Hausdorff空間,並且G上的乘法運算與求逆運算
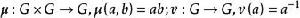 軌道空間
軌道空間都是連續的。
定義2 如果G和H是兩個拓撲群,設G×H表示兩個群的直積,帶上積拓撲,則G×H也是一個拓撲群 。
定義3 設G是一個拓撲群,稱G如同一個同胚群而作用於拓撲空間X,是指G的每個元素g都誘導一個同胚 ,並且滿足下列條件:
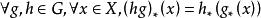 軌道空間
軌道空間(1) ;
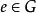 軌道空間
軌道空間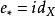 軌道空間
軌道空間(2) 若 為單位元,則e誘導恆同同胚,即 ;
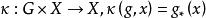 軌道空間
軌道空間(3) 映射 連續。
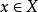 軌道空間
軌道空間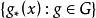 軌道空間
軌道空間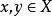 軌道空間
軌道空間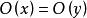 軌道空間
軌道空間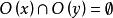 軌道空間
軌道空間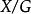 軌道空間
軌道空間若G如同一個同胚群而作用於拓撲空間X,則對於每個 ,集合 稱為x的 軌道,記為 。很顯然,對於任意兩個點 ,要么 ,要么 。因此所有的軌道實際上給出了空間X的一個劃分,由此可以確定一個商空間(即把每個軌道粘合成一個點的粘合空間),稱為該作用的 軌道空間,記為 。
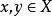 軌道空間
軌道空間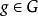 軌道空間
軌道空間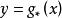 軌道空間
軌道空間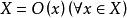 軌道空間
軌道空間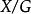 軌道空間
軌道空間如果對於任意兩個點 ,都存在一個 使得 ,則稱G在拓撲空間X的作用是 可遷的,顯然,此時 ,因此 是單點空間 。
舉例分析
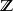 軌道空間
軌道空間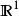 軌道空間
軌道空間例1 (1)考慮無限循環群 在 上的如下作用:
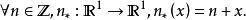 軌道空間
軌道空間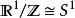 軌道空間
軌道空間容易驗證,其軌道空間 。
 軌道空間
軌道空間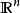 軌道空間
軌道空間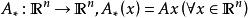 軌道空間
軌道空間 軌道空間
軌道空間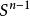 軌道空間
軌道空間(2) 設n≥2,考慮正交群 ,線上性代數中我們已經知道,每個 都確定了 中的一個線性變換 ,這個線性變換保持歐氏度量。特別地,把單位向量映射為單位向量。因此每個 誘導了 的一個自同胚。並且容易看出,映射
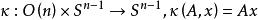 軌道空間
軌道空間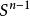 軌道空間
軌道空間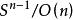 軌道空間
軌道空間是連續的。因此, 如同一個同胚群作用於球面 上。由Schmidt正交化方法不難看出,這個作用還是可遷的,因此軌道空間 只有一個點。
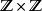 軌道空間
軌道空間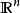 軌道空間
軌道空間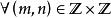 軌道空間
軌道空間(3) 考慮群 在平面 上的作用: ,定義一個同胚
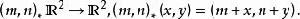 軌道空間
軌道空間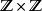 軌道空間
軌道空間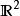 軌道空間
軌道空間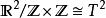 軌道空間
軌道空間容易驗證,上述對應確實給出了 在平面 上的一個作用。由(1)可知,其軌道空間是兩個圓周的積空間。而且不難看出,平面上每個邊長為1的正方形都包含了每個軌道中的點,並且正方形的對邊在軌道空間中顯然被同向地粘合在了一起,因此又有 。
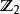 軌道空間
軌道空間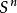 軌道空間
軌道空間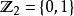 軌道空間
軌道空間(4)考慮剩餘類群 在n-維球面 上的作用:不妨記 ,其中0為單位元,而1為生成元。定義兩個同胚;
 軌道空間
軌道空間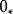 軌道空間
軌道空間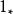 軌道空間
軌道空間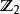 軌道空間
軌道空間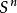 軌道空間
軌道空間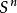 軌道空間
軌道空間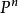 軌道空間
軌道空間就是恆等同胚, 就是對徑映射,也是同胚。則不難驗證,上述定義給出了 在n-維球面 上的一個作用,其軌道空間正是粘合 的對徑點而得到的n-維射影平面 。
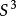 軌道空間
軌道空間(5) 設p,q是兩個互質的整數,把3-維球面 看做2-維復空間內的單位球面,即
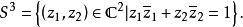 軌道空間
軌道空間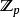 軌道空間
軌道空間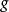 軌道空間
軌道空間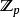 軌道空間
軌道空間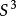 軌道空間
軌道空間設 的生成元為 ,定義 在 上的作用如下:
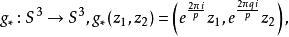 軌道空間
軌道空間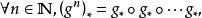 軌道空間
軌道空間(幾次複合).
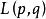 軌道空間
軌道空間則不難驗證,這確實給出了一個群作用,其軌道空問稱為 透鏡空間,記為 。
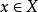 軌道空間
軌道空間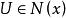 軌道空間
軌道空間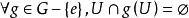 軌道空間
軌道空間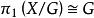 軌道空間
軌道空間定理 如G一個同胚群而作用於單連通空間X,並且對於每個點 ,都存在 使得 ,則 。
利用這個定理,我們也可以得到下面幾個結論
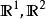 軌道空間
軌道空間 軌道空間
軌道空間例2 由於 及 都是單連通的,因此由例1可知 ,
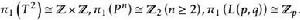 軌道空間
軌道空間
