簡介
設M是內積空間X的一個不含零子集,若M中向量兩兩正交,則稱M為X中的正交系,又若M中向量的範數都為1,則稱M為X中的規範正交系。
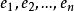 規範正交系
規範正交系元素的正交性在內積空間和Hilbert空間中扮演著十分重要的角色。在n維歐氏空間,選定n個相互正交的向量 ,則形成n維空間中的一組正交基,也就是說在空間中建立了一組坐標系,空間中的任何一個元素都可以由這組坐標的線性組合表示出來。
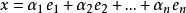 規範正交系
規範正交系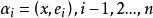 規範正交系
規範正交系其中 。
R 為n維歐氏空間,則向量集
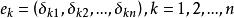 規範正交系
規範正交系為R 中規範正交系,其中
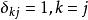 規範正交系
規範正交系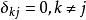 規範正交系
規範正交系基本性質
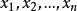 規範正交系
規範正交系(1)對正交系M中任意有限個向量 ,有
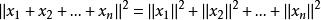 規範正交系
規範正交系事實上,由於M中向量兩兩正交,所以
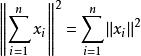 規範正交系
規範正交系(2)正交系M是X中線性無關子集。
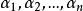 規範正交系
規範正交系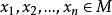 規範正交系
規範正交系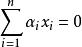 規範正交系
規範正交系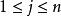 規範正交系
規範正交系事實上,設 ,而且 ,其中為n個數,則對任何 ,有
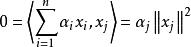 規範正交系
規範正交系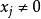 規範正交系
規範正交系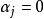 規範正交系
規範正交系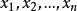 規範正交系
規範正交系由於 ,因此 ,所以 線性無關,從而說明M是X中線性無關子集。
套用
在傅立葉係數
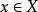 規範正交系
規範正交系設M為內積空間X中的規範正交系,,稱數集
 規範正交系
規範正交系為向量x關於規範正交系M的傅立葉係數集。
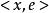 規範正交系
規範正交系而稱為x關於e傅立葉係數。
在Bessel不等式
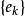 規範正交系
規範正交系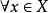 規範正交系
規範正交系設是內積空間中的有限或可數規範正交系,則對,有
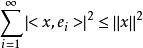 規範正交系
規範正交系在級數
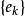 規範正交系
規範正交系設是Hilbert空間中的可數規範正交系,則
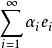 規範正交系
規範正交系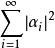 規範正交系
規範正交系(1)級數收斂的充要條件為級數收斂。
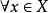 規範正交系
規範正交系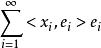 規範正交系
規範正交系(2)對,級數收斂。
舉例
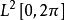 規範正交系
規範正交系在空間 中,定義內積為
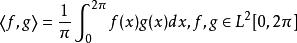 規範正交系
規範正交系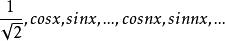 規範正交系
規範正交系 規範正交系
規範正交系則三角函式系 為 中規範正交系,所以內積空間中規範正交系是正交函式系概念的推廣。
