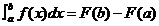萊布尼茨公式理解：
比如路程公式： 距離s=速度v*時間t，即s=v*t，那么如果t是從時間a開始計算到時間b為止，t=b-a，而如果v不能在這個時間段內保持均速，那么上面的這個公式（s=v*t，t=b-a）就不能和諧的得到正確結果，於是引出了定積分的概念。
那么如何在用積分得到上述路程公式呢？
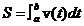公式牛頓-萊布尼茨公式的意義就在於把不定積分與定積分聯繫了起來，也讓定積分的運算有了一個完善、令人滿意的方法。下面就是該公式的證明全過程：[title]對函式f(x)於區間[a,b]上的定積分表達為：[/title]b∫a*f(x)dx
現在我們把積分區間的上限作為一個變數，這樣我們就定義了一個新的函式：
Φ(x)= x∫a*f(x)dx
但是這裡x出現了兩種意義，一是表示積分上限，二是表示被積函式的自變數，但定積分中被積函式的自變數取一個定值是沒意義的。為了只表示積分上限的變動，我們把被積函式的自變數改成別的字母如t，這樣意義就非常清楚了：
Φ(x)= x∫a*f(t)dt
研究這個函式Φ(x）的性質： 1、定義函式Φ(x)= x(上限)∫a（下限）f(t)dt，則Φ 與格林公式和高斯公式的聯繫
’(x)=f(x)。
證明：讓函式Φ(x)獲得增量Δx，則對應的函式增量
ΔΦ=Φ(x+Δx)-Φ(x)=x+Δx(上限)∫a（下限）f(t)dt-x(上限)∫a（下限）f(t)dt
顯然，x+Δx(上限)∫a（下限）f(t)dt-x(上限)∫a（下限）f(t)dt=x+Δx(上限)∫x（下限）f(t)dt
而ΔΦ=x+Δx(上限)∫x（下限）f(t)dt=f(ξ)·Δx(ξ在x與x+Δx之間，可由定積分中的中值定理推得，
也可自己畫個圖，幾何意義是非常清楚的。)
當Δx趨向於0也就是ΔΦ趨向於0時，ξ趨向於x，f(ξ)趨向於f(x)，故有lim Δx→0 ΔΦ/Δx=f(x)
可見這也是導數的定義,所以最後得出Φ’(x)=f(x)。
2、b(上限)∫a（下限）f(x)dx=F（b）-F（a），F（x）是f(x)的原函式。
證明：我們已證得Φ’(x)=f(x)，故Φ(x）+C=F（x）
但Φ(a)=0（積分區間變為[a,a]，故面積為0），所以F（a）=C
於是有Φ(x）+F（a）=F（x），當x=b時，Φ(b)=F（b)-F(a),
而Φ(b)=b(上限)∫a（下限）f(t)dt，所以b(上限)∫a（下限）f(t)dt=F（b)-F(a)
把t再寫成x，就變成了開頭的公式，該公式就是牛頓-萊布尼茨公式。
高階導數萊布尼茲公式
(uv)^(n)=∑(n，k=0) C(k,n) * u^(n-k) * v^(k)
註：
C(k,n)=n!/(k!(n-k)!)
^代表後面括弧及其中內容為上標，求xx階導數
