空間反演變換Space reversal transformation空間反演是把所有的坐標改變符號(即
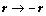 空間反演變換
空間反演變換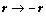
在平面內設有一半徑為R,中心為O的圓,對任一異於O點的P點,將其變換成該射線OP上一點P┡,且使OP┡·OP=R,這個變換叫做平面反演變換。圓O叫做反演基圓,圓心O 叫做反演中心或反演極,R 叫做反演半徑或反演冪,從定義可知,反演變換將過反演中心的射線變成自身,且在此射線上建立對合對應,它使位於圓內的點變成圓外的點,位於圓外的點變成圓內的點,反演中心變成平面內的無限遠點。而反演圓上的點則保持不變。空間反演變換可以看作是平面反演變換繞反演基圓的直徑旋轉而得。反演變換下,將不過反演中心的直線或平面,分別變成過反演中心的圓或球面;將不過反演中心的圓或球面,分別變成另一個不過反演中心的圓或球面。反之也成立。反演變換是反向保角的,即使兩線(或兩面)所成的角度的大小保持不變,但方向相反。
空間反演變換Space reversal transformation空間反演是把所有的坐標改變符號(即
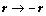 空間反演變換
空間反演變換空間反演是把所有的坐標改變符號(即空間反演變換)的操作。
初等幾何變換,是一個將幾何圖形按照某種法則或規律變成另一種幾何圖形的過程。它對於幾何學的研究有重要作用。初等幾何變換主要包括全等變換,相似變換,反演變換。
概念解釋 全等變換 相似變換 反演變換P變換的概括
的規律,也就是說力學規律對於鏡象反演不變,具有空間反演不變性。同樣對於麥克斯韋方程組和薛丁格方程都具有空間反演不變性。不變性原理通常與守恆定律...。為了描述這種與空間反演對稱性相聯繫的物理量,引入了“宇稱”的概念。因為...
原理 不變性 τ-θ之謎。空間反演是指空間坐標相對於坐標原點的變換,即將坐標 x、y、z 換成-x、-y、-z的變換。空間反演對稱性導致宇稱守恆。然而在弱相互作用下,粒子的運動...研究物理規律的特徵,並給以精確化,把它與變換聯繫起來。通常把兩種情況通過...
簡介 對稱性 諾特定理 意義的世界與真實世界的變換稱為空間反演. 宇稱守恆就是(物理規律)在空間反演...的變換稱為時間反演. 宙稱守恆就是(物理規律)在時間反演下不變...
概念1932年,Wigner在量子力學中引進了時間反演,乍一看來,這是與空間反演相似的一個分立對稱性,實際上不然。這是用詞不當。嚴格地說,所謂...定義,讓我們先作變換 ,看變換後對 的薛丁格方程是否能保持與原來有同樣形式...
概念 基本原理基本關係第1點 內涵關係時、空、質在內涵上是既各自獨立又相互聯繫著的三個絕對概念。時間公理、空間點分理、質量總體分理表達了它們的...
基本關係 理論解釋 基本概念 牛頓的時空觀 相對論時空的變換行為。 和空間反演的情形相似,根據物理方程中出現時間反演下倒向...對稱點群理論和不可逆過程中的昂薩格原理的建立,又將這種方法從空間對稱變換...張量的空間變換規律 各向異性晶體物理性能的數學描述的手段是張量。晶體...
晶體物理性能的對稱性 正文 配圖 相關連線