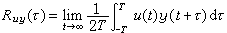相關函式

相關函式，是指兩個信號之間相似性的一種量度。信號可以是確定性的，也可以是隨機性的。

相關函式

正文

對於兩個確定性的連續信號u(t)和y(t),如果它們在(-∞,+∞)上是平方可積的,則它們的互相關函式是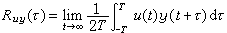

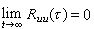實際上經常會遇到u(t)和y(t)是由同一個信號源產生的兩個信號的情況,例如地震勘探信號、雷達發射與接收的回波信號等。通過計算互相關函式可以比較和分辨它們的相似程度。如果u(t)和y(t)是同一信號,則稱Ruu(τ)為信號u(t)的自相關函式。自相關函式主要有以下性質：①|Ruu(τ)|≤Ruu(0)；②；③Ruu(τ)是τ的偶函式,即Ruu(-τ)=Ruu(τ)；④Ruu(τ)的形狀與信號u(t)中的各種頻率成分有關。互相關函式的性質與自相關函式有明顯的不同:①Ruy(0)不一定是Ruy(τ)的極大值;②Ruy(τ)不是τ的偶函式;③Ruy(τ)只與u(t)和y(t)中共同的頻率成分有關。如果信號是離散的無窮序列ut和yt，則互相關與自相關函式序列分別是

和

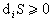
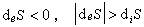它們也分別具有上述的性質。如果函式u(t)和y(t)都是以T為周期的,或序列{ut}和{yt}都是以N為循環長度的，則它們的循環相關函式也是周期的或循環的，其計算可以簡化為
　 $$!!或　

這種循環相關函式仍然具有上述性質。
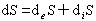
對於兩個隨機性的續信號連u(t)和y(t),它們的相關函式是由數學期望給出的：Ruy(τ)＝E【u(t)y(t+τ)】和Ruu(τ)＝E【u(t)u(t+τ)】,其中E【·】代表對括弧內的隨機變數求數學期望。這時的相關函式仍然具有前述的幾條性質。
有時，對於隨機信號的一個樣本函式也可以規定它的按時間平均的相關函式，這種按時間平均的相關函式與用數學期望規定的隨機信號的相關函式是不相同的。但如果隨機信號是平穩遍歷的，則以機率平均（即數學期望）規定的相關函式與用時間平均規定的相關函式是幾乎處處相等的。這時，可以由隨機信號的樣本值以時間平均的相關函式來計算隨機信號在機率平均意義下的相關函式，即

配圖

相關連線